Áp dụng hàm số cos, ta có: \(BC=\sqrt{6^2+12^2-2.6.12.\cos120^o}\)

\(d_a=\frac{2}{b+c}\sqrt{bc\left(p-a\right)}\)

Đến đây bạn tự làm nhé!

Qua D kẻ DE // AB ( E \(\in\)AB )

Vì AD là phân giác góc A của \(\Delta ABC\):

\(\Rightarrow\)\(\frac{DC}{DB}=\frac{AC}{AB}\)

\(\Rightarrow\) \(\frac{DC}{DB+DC}=\frac{AC}{AB+AC}\)hay \(\frac{DC}{BC}=\frac{6}{3+6}\)\(\Leftrightarrow\)\(\frac{DC}{BC}=\frac{2}{3}\)(1)

Ta có : AB là phân giác góc A \(\Rightarrow\)\(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{BAC}}{2}=\frac{120}{2}=60^0\)

Mà \(\widehat{A_1}=\widehat{D_1}=60^0\)( so le trong , DE // AB )

\(\Rightarrow\widehat{A_2}=\widehat{D_1}=60^0\Rightarrow\)\(\Delta ADE\)đều

\(\Rightarrow\)AD = DE 

Vì DE // AB ( cách dựng )

Xét \(\Delta ABC\)theo hệ quả định lý Ta-lét ta có:\(\frac{DE}{AB}=\frac{DC}{BC}\)(2)

Thế (1) vào (2) ta được :\(\frac{DE}{AB}=\frac{2}{3}\)hay \(\frac{DE}{3}=\frac{2}{3}\)

\(\Rightarrow DE=\frac{2.3}{3}=2\left(cm\right)\)

\(\Rightarrow AD=2\left(cm\right)\)( AD=DE chứng minh trên )

11:

\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)

12:

\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)

AB=5

HC=5

AH^2+AB^2=AB^2

AC^2-BH^2=HC^2

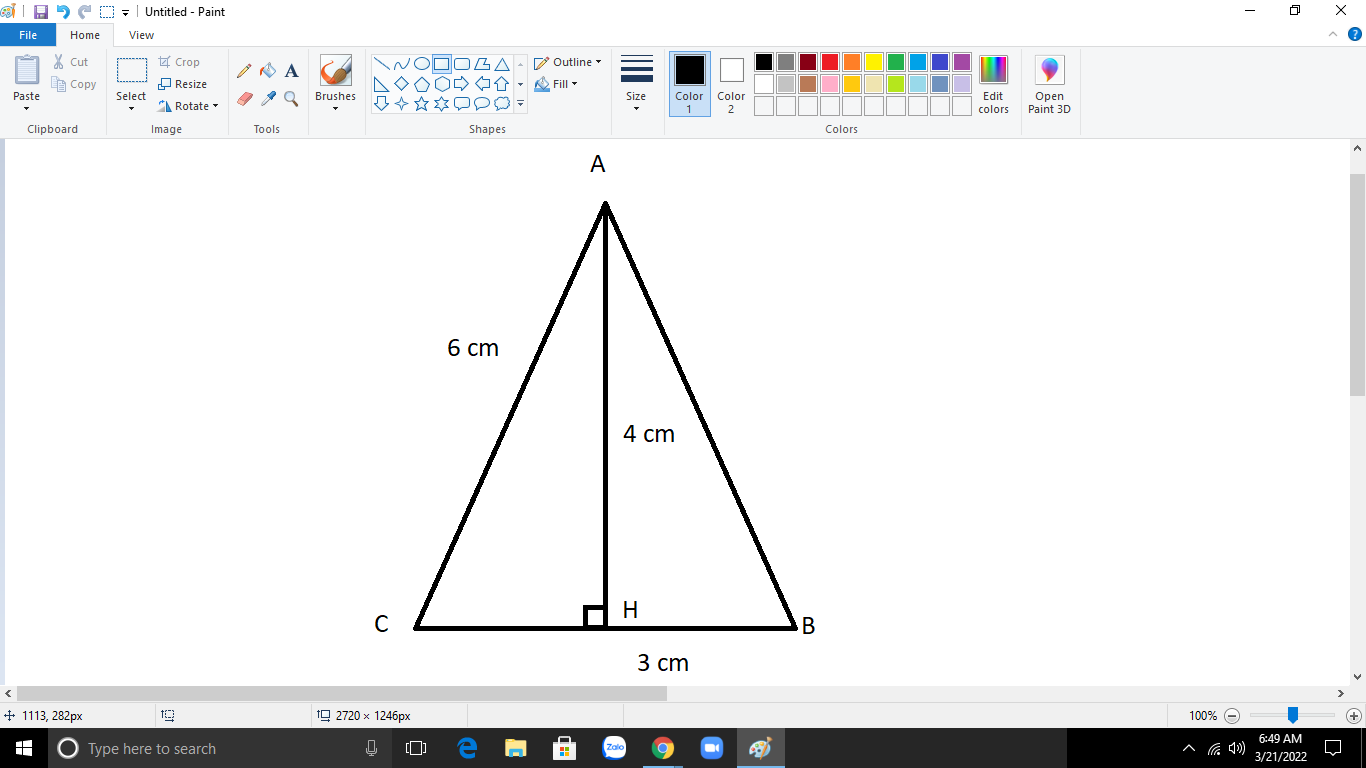
\(\text{Xét }\Delta AHB\text{ vuông tại H có:}\)

\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)

\(\Rightarrow AB^2=4^2+3^2=16+9=25\left(cm\right)\)

\(\Rightarrow AB=\sqrt{25\left(cm\right)}=5\left(cm\right)\)

\(\text{Xét }\Delta AHC\text{ có:}\)

\(AC^2=AH^2+HC^2\)

\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)

\(\Rightarrow HC^2=6^2-4^2=36-16=20\left(cm\right)\)

\(\Rightarrow HC=\sqrt{20}\left(cm\right)\)

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có

góc C chung

=>ΔCDE đồng dạng với ΔCAB

b: BC=căn 3^2+5^2=căn 34(cm)

AD là phân giác

=>BD/AB=CD/AC

=>BD/3=CD/5=căn 34/8

=>BD=3/8*căn34(cm)

c: \(AD=\dfrac{2\cdot5\cdot3}{5+3}\cdot cos45=\dfrac{15}{8}\cdot\sqrt{2}\left(cm\right)\)