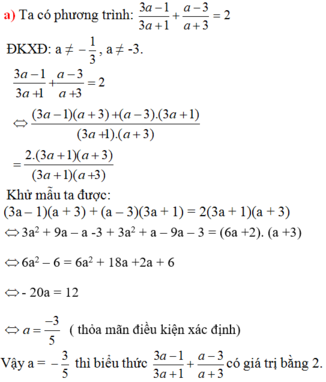a) \(\frac{2a^2-3a-2}{a^2-4}=2\)

\(\Rightarrow2a^2-3a-2=2\left(a^2-4\right)\)

\(\Rightarrow2a^2-3a-2=2a^2-4\)

\(\Rightarrow-3a-2=-4\)

\(\Rightarrow-3a=-2\Rightarrow a=\frac{2}{3}\)

b) \(\frac{3a-1}{3a+1}+\frac{a-3}{a+3}=2\)

\(\Rightarrow\frac{\left(3a-1\right)\left(a+3\right)+\left(3a+1\right)\left(a-3\right)}{\left(3a+1\right)\left(a+3\right)}=2\)

\(\Rightarrow\frac{6a^2-6}{3a^2+10a+3}=2\)

\(\Rightarrow6a^2-6=2\left(3a^2+10a+3\right)\)

\(\Rightarrow6a^2-6=6a^2+20a+6\)

\(\Rightarrow-6=20a+6\Rightarrow20a=-12\)

\(\Rightarrow a=\frac{-3}{5}\)

a, \(\frac{2a^2-3a-2}{a^2-4}=2\)

\(\Leftrightarrow\frac{a\left(2a+1\right)-2\left(2a+1\right)}{a^2-4}=2\)

\(\Leftrightarrow\frac{\left(a-2\right)\left(2a+1\right)}{a^2-2^2}=2\)

\(\Leftrightarrow\frac{\left(a-2\right)\left(2a+1\right)}{\left(a-2\right)\left(a+2\right)}=2\)

\(\Leftrightarrow\frac{2a+1}{a+2}=2\)

\(\Leftrightarrow2a+1=2\left(a+2\right)\Leftrightarrow2a+1=2a+4\Leftrightarrow2a+1-2a-4=0\)

\(\Leftrightarrow-3\ne0\)(voli)

b, \(\frac{3a-1}{3a+1}+\frac{a-3}{a+3}=2\)

\(\Leftrightarrow\frac{\left(3a-1\right)\left(a+3\right)}{\left(3a+1\right)\left(a+3\right)}+\frac{\left(a-3\right)\left(3a+1\right)}{\left(a+3\right)\left(3a+1\right)}=\frac{2\left(3a+1\right)\left(a+3\right)}{\left(3a+1\right)\left(a+3\right)}\)

\(\Leftrightarrow\left(3a-1\right)\left(a+3\right)+\left(a-3\right)\left(3a+1\right)=2\left(3a+1\right)\left(a+3\right)\)

\(\Leftrightarrow6a^2-6=6a^2+20a+6\)

\(\Leftrightarrow6a^2-6-6a^2-20a-6=0\)

\(\Leftrightarrow-12-20a=0\)

\(\Leftrightarrow20a=-12\)

\(\Leftrightarrow a=-\frac{3}{5}\)

\(ĐKXĐ:\)\(a\ne-3\)\(;a\ne\frac{-1}{3}\)

\(\frac{3a-1}{3a+1}+\frac{a-3}{a+3}=\)\(2\)

\(\Leftrightarrow\frac{\left(3a-1\right)\left(a+3\right)}{\left(3a+1\right)\left(a+3\right)}+\frac{\left(3a+1\right)\left(a-3\right)}{\left(3a+1\right)\left(a+3\right)}\)\(=\frac{2\left(3a+1\right)\left(a+3\right)}{\left(3a+1\right)\left(a+3\right)}\)

\(\Leftrightarrow\left(3a-1\right)\left(a+3\right)+\left(3a+1\right)\left(a-3\right)-2\left(3a+1\right)\left(a+3\right)\)\(=0\)

\(\Leftrightarrow3a^2+9a-a-3+3a^2-9a+a-3-6a^2-18a-2a-6\)\(=0\)

\(\Leftrightarrow\left(3a^2+3a^2-6a^2\right)+(9a-a-9a+a-18a-2a)-\left(3+3+6\right)\)\(=0\)

\(\Leftrightarrow-20a-12=0\)

\(\Leftrightarrow-20a=12\)

\(\Leftrightarrow a=\frac{-12}{20}=\frac{-3}{5}\)( thỏa mãn )

\(Vậy\) \(a=\frac{-3}{5}\)khi biểu thức có giá trị là 2

Lời giải:
ĐKXĐ: $a\neq \frac{-1}{3}; a\neq -3$

Ta có:

$\frac{3a-1}{3a+1}+\frac{3-a}{3+a}=2$

$\Leftrightarrow \frac{3a-1}{3a+1}-1=1-\frac{3-a}{3+a}$

$\Leftrightarrow \frac{-2}{3a+1}=\frac{2a}{a+3}$

$\Rightarrow -2(a+3)=2a(3a+1)$

$\Leftrightarrow 6a^2+2a+2a+6=0$
$\Leftrightarrow 6a^2+4a+6=0$

$\Leftrightarrow 3a^2+2a+3=0$

$\Leftrightarrow (a^2+2a+1)+2a^2+2=0$

$\Leftrightarrow (a+1)^2+2a^2=-2<0$ (vô lý - loại)

Vậy PT vô nghiệm.

a) \(ĐK:a\ne1;a\ne0\)

\(A=\left[\frac{\left(a-1\right)^2}{3a+\left(a-1\right)^2}-\frac{1-2a^2+4a}{a^3-1}+\frac{1}{a-1}\right]:\frac{a^3+4a}{4a^2}=\left[\frac{a^2-2a+1}{a^2+a+1}-\frac{1-2a^2+4a}{a^3-1}+\frac{a^2+a+1}{a^3-1}\right].\frac{4a^2}{a^3+4a}\)\(=\left[\frac{a^3-3a^2+3a-1}{a^3-1}-\frac{1-2a^2+4a}{a^3-1}+\frac{a^2+a+1}{a^3-1}\right].\frac{4a^2}{a^3+4a}=\frac{a^3-1}{a^3-1}.\frac{4a}{a^2+4}=\frac{4a}{a^2+4}\)

b) Ta có: \(a^2+4\ge4a\)(*)

Thật vậy: (*)\(\Leftrightarrow\left(a-2\right)^2\ge0\)

Khi đó \(\frac{4a}{a^2+4}\le1\)

Vậy Max_A = 1 khi x = 2

•๖ۣۜIηεqυαℓĭтĭεʂ•ッᶦᵈᵒᶫ★T&T★ Idol cho em hỏi là, cái chỗ \(\left(a-2\right)^2\ge0\) thì tại sao Khi đó: \(\frac{4a}{a^2+4}\le1\)

Mong Idol pro giải thích hộ em chỗ này :((

À dạ thôi oke, em hiểu rồi((: 

Biểu thức có giá trị bằng 2 thì: