cho tam giác DEFcó DE<DF.Vẽ đường cao DH
a/So sánh HE và HF
b/Trên DH lấy điểm M.So sánh ME và MF.
Những câu hỏi liên quan
Cho tam giác ADE cân tại A. K là tđ của DE
a)C/m: tam giác ADK=tam giác AEK
b)C/m: AK_|_ DE
c) Trên AD lấy B, Ac lấy C sao cho BD=CE. C/m:tam giác BDE=tam giác CED
d)C/m:BC//DE
Cho tam giác abc vuông tại a, AB<BC. BD là tia phân giác của góc B, D thuộc AC.Từ D kẻ DE vuông góc BC tại E.
a) Chứng minh tam giác ABC=tam giác EBD
b) Kéo dài DE và AB sao cho cắt nhau tại F. Chứng minh tam giác CDF cân
c) Chứng minh DE<DF
Cho tam giác ABC có A = 90 độ ( AB < AC ) , đường cao AH, AD là phân giác của tam giác AHC kẻ DE vuông góc với AC
a. Chứng minh DE = DH b.Gọi K là giao điểm của DE và AH. Chứng minh tam giác AKC cann c. Chứng minh tam giác KEH tam giác CEH d. Cho BH = 8 cm CH = 32cm. Tính AC
e. Giả sử tam giác ABC = 30 độ, AD cắt CK tại P. chứng minh tam giác HEP đều
Cho tam giác MNP = tam giác DEF. Tìm các cạnh bằng nhau giữa hai tam giác ?
MN = DE; MP= DF; NP = EF.
MN = DF; MP= DE; NP = EF.
MN = EF; MP= DF; NP = ED.
MN = DE; MP= EF; NP = DF.
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D.a) Cho biết BC10cm, AB6cm, AD3cm. Tính AC, CDb)Vẽ DE vuông góc với BC tại F. CM: tam giác ABD tam giác EBD và tam giác BAE cânc) Gọi F là giao điểm của AB và DE. So sánh DE và DFd)Gọi H là giao điểm của BD và CF. K là điểm trên tia đối của tia DF sao cho DK DF. I là điểm trên đoạn thẳng CD sao cho CI 2DI. CM:K, H, I thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D.
a) Cho biết BC=10cm, AB=6cm, AD=3cm. Tính AC, CD
b)Vẽ DE vuông góc với BC tại F. CM: tam giác ABD= tam giác EBD và tam giác BAE cân
c) Gọi F là giao điểm của AB và DE. So sánh DE và DF
d)Gọi H là giao điểm của BD và CF. K là điểm trên tia đối của tia DF sao cho DK = DF. I là điểm trên đoạn thẳng CD sao cho CI = 2DI. CM:K, H, I thẳng hàng
13 tháng 2 2020 lúc 16:52
cho tam giác ABC vuông tại A qua D thuộc cạnh bC kẻ đoạn DE nhằm ngoài tam giác ABC sao cho DE//AC vad DE=4cm , tính Sabc
13 tháng 2 2020 lúc 17:24
cho tam giác ABC vuông tại A qua D thuộc cạnh bC kẻ đoạn DE nhằm ngoài tam giác ABC sao cho DE//AC vad DE=4cm , tính Sabc
cho tam giác ABC vuông tại A qua D thuộc cạnh bC kẻ đoạn DE nhằm ngoài tam giác ABC sao cho DE//AC vad DE=4cm , tính Sabc
Cho tam giác ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho DB = EC < 1/2 DE. Tam giác ABC là tam giác gì? Chứng minh điều đó?
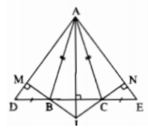
Do ΔADE cân tại A nên ∠D =∠E
Xét ΔABD và ΔACE, ta có:
AD = AE (gt)
∠D =∠E (chứng minh trên)
DB=EC (gt)
Suy ra: ΔABD= ΔACE(c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy: ΔABC cân tại A
Đúng 0
Bình luận (0)