Cho tam giác ABC có AB=2cm,AC=3cm,BC=4cm,phân giác AD. Tính độ dài của BD và CD

Những câu hỏi liên quan
Bài 2. (2 điểm)a) Tính độ dài x trong hình vẽ (Biết DE // BC )b. Cho tam giác ABC có AB 2cm, AC 3cm, BC 4 cm, phân giác AD. Tính độ dài của BD và CD.
Đọc tiếp
Bài 2. (2 điểm)
a) Tính độ dài x trong hình vẽ (Biết DE // BC )
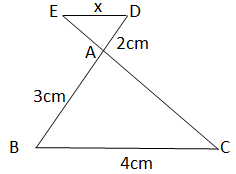
b. Cho tam giác ABC có AB = 2cm, AC = 3cm, BC = 4 cm, phân giác AD. Tính độ dài của BD và CD.
a | Áp dụng hệ quả của định lý Ta-lét ta có: 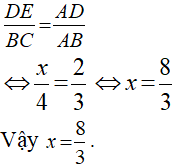 |
b | Ta có: 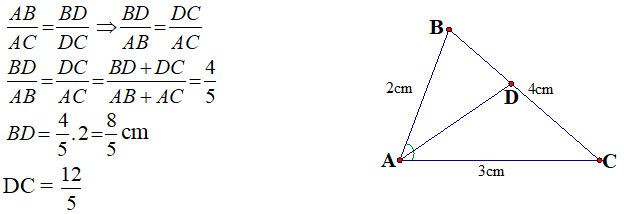 |
Đúng 2
Bình luận (0)
a | Áp dụng hệ quả của định lý Ta-lét ta có: 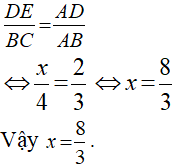 |
b | Ta có:  |
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A, có đường cao AH, tia phân giác AD của góc BAC (D thuộc BC) biết AB =3cm; AC =4cm. Tính độ dài BD và DC, mong mn giúp nhé!
BC=căn 3^2+4^2=5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4
=>BD/3=CD/4=5/7
=>BD=15/7cm; CD=20/7cm
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, có đường cao AH, tia phân giác AD của góc BAC (D thuộc BC) biết AB =3cm; AC =4cm. Tính độ dài BD và DC, mong mn giúp nhé!
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB<AC. Đường phân giác AD, đường trung trực của AD cắt BC tại K.
a, Chứng minh rằng tam giác KAB đồng dạng với tam giác KCA
b, Tính độ dài đoạn KD, biết độ dài cạnh BD là 2cm và độ dài cạnh CD là 4cm
ai trả lời nhanh và chi tiết nhất sẽ dùng 2 nick để li-ke ạ (thề danh dự)
Cho Δ ABC có AD là đường phân giác của góc B A C ^ ( D ∈ BC ) sao cho DB = 2cm, có AB = 3cm, AC = 4cm. Tính độ dài cạnh DC.
Áp dụng định lí trên ta có: Δ ABC, AD là đường phân giác của góc B A C ^ ( D ∈ BC )
Ta có DB/AB = DC/AC hay 2/3 = DC /4 ⇒ DC = (2.4)/ 3 = 8/3 = 2,(6 ) ( cm )
Đúng 0
Bình luận (0)
Cho Δ ABC có AD là đường phân giác của góc B A C ^ ( D ∈ BC ) sao cho DB = 2cm, có AB = 3cm, AC = 4cm. Tính độ dài cạnh DC.
Áp dụng định lí trên ta có: Δ ABC, AD là đường phân giác của góc B A C ^ ( D ∈ BC )
Ta có DB/AB = DC/AC hay 2/3 = DC /4 ⇒ DC = (2.4)/ 3 = 8/3 = 2,(6 ) ( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB=3cm, AC=4cm, đường phân giác AD .Đường vuông góc với DC cắt AC ở E
a/ C/m rằng tam giác ABC và tam giác DEC đồng dạng
b/ Tính độ dài các đoạn thẳng BC, BD
c/ Tính độ dài AD
d/ Tính diện tích tam giác ABC và diện tích tứ giác ABDE
Cho tam giác ABC vuông tại A, có AB=3cm,AC=4cm. Kẻ đường phân giác BD của góc ABC.
a) Tính BC, AD, DC
b) Trên BC lấy điểm E sao cho CE=2cm. CM tam giác CED ~ tam giác CAB
c) Chứng minh ED=AD
a) áp dụng định lí pitago vào tam giác abc được ab2 +ac2=bc2 suy ra bc2= 32+42=25 suy ra bc=5
có bd là phân giác góc abc nên ab/ad=bc/dc
dùng tính chất dãy tỉ số bằng nhau ta có ab/ad=bc/dc=(ab+bc)/(ad+dc)=(3+5)/4=2
nên ad=ab/2=3/2
dc=bc/2=5/2
b) dựa vào số đo độ đài cm được ec/ac=dc/bc
xét tam giác abc vuông và tam giác edc vuông có góc c chung và ea/ac=dc/bc nên suy ra 2 tam giác đó đồng dạng
c) tg abc và tg edc đồng dạng suy ra de vuông góc với bc
bd là phân giác abc có de vuông góc với bc, da vuông góc với ab nên suy ra de=da (tính châts này đã học ở lớp 7)
Đúng 1
Bình luận (0)
Cho ABC vuông tại A có AB = 3cm, AC = 4cm a) tính độ dài cạnh BC? b) vẽ phân giác BD (D thuộc AC) từ D vẽ DE vuông góc BC (E thuộc BC) chứng minh Tam giác ABD = tam giác EBD c) chứng minh BD + CD>2.DA
a: BC=căn 3^2+4^2=5cm
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔABD=ΔEBD
Đúng 0
Bình luận (0)















