So sánh các góc của tam giác ABC biết rằng: AB=4cm, AC=6cm, BC=5cm

Những câu hỏi liên quan
hãy so sánh các góc của tam giác ABC biết AB=6cm AC= 4cm và BC = 5cm ?
Ta có:\(AB>AC< BC\)
\(\Leftrightarrow\widehat{C}>\widehat{A}>\widehat{B}\)
So sánh các góc của tam giác ABC, biết rằng:
AB = 2cm, BC = 4cm, AC = 5cm
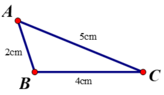
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
Đúng 0
Bình luận (0)
So sánh các góc của tam giác ABC biết a)AB=6cm, BC=6cm, AC=4cm b)Tam giác ABC vuông tại B có AB=6cm, AC=10cm
So sánh các góc của tam giác ABC biết a)AB=6cm, BC=6cm, AC=4cm b)Tam giác ABC vuông tại B có AB=6cm, AC=10cm
a) Xét ΔABC có AB=BC>AC(6cm=6cm>4cm)
mà góc đối diện với cạnh AB là góc ACB
và góc đối diện với cạnh BC là góc BAC
và góc đối diện với cạnh AC là góc ABC
nên \(\widehat{ACB}=\widehat{BAC}>\widehat{ABC}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
b) Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=AB^2+BC^2\)
\(\Leftrightarrow BC^2=AC^2-AB^2=10^2-6^2=64\)
hay BC=8(cm)
Xét ΔABC có AB<BC<AC(6cm<8cm<10cm)
mà góc đối diện với cạnh AB là góc ACB
và góc đối diện với cạnh BC là góc BAC
và góc đối diện với cạnh AC là góc ABC
nên \(\widehat{ACB}< \widehat{BAC}< \widehat{ABC}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
So sánh các góc của tam giác ABC, biết rằng :
AB = 2cm, BC = 4cm, AC = 5cm
Trong tam giác ABC có:
AB = 2cm ; BC = 4cm ; AC = 5cm
=> AB < BC < CA nên
Đúng 0
Bình luận (0)
So sánh các góc của tam giác ABC, biết rằng:
AB = 2cm, BC = 4cm, AC = 5 cm.
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm
=> AB < BC < CA => ˆC<ˆA<ˆB
Đúng 0
Bình luận (0)
Tam giác ABC có
AC > BC > AB (5cm>4cm>2cm)
nên ^B > ^A > ^C (quan hệ giữa góc và cạnh đối diện)
Đúng 0
Bình luận (0)
So sánh các góc của tam giác ABC biết rằng AB = 5cm, BC = 5cm, AC = 3cm.
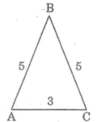
Ta có: AB = BC nên ΔABC cân tại B
Suy ra: ∠A = ∠C
Vì BC > AC nên ∠A > ∠B (đối diện cạnh lớn hơn là góc lớn hơn)
Vậy ∠A = ∠C > ∠B .
Đúng 0
Bình luận (0)
So sánh các góc của tam giác ABC biết rằng AB=5cm,BC=5cm,AC=3cm
So sánh các góc của tam giác ABC biết rằng AB = 5cm, BC = 5cm, AC = 3cm.
Ta có : AB = 5cm ; BC = 5cm ; AC = 3cm
\(\Rightarrow\)AB = BC = 5cm
AB > AC ( 5cm > 3cm )
AC < BC ( 3cm < 5cm )
Chúc bn hok tốt
Đúng 0
Bình luận (0)
Ta có: AB = BC nên ΔABC cân tại B
Suy ra: \(\widehat{A}=\widehat{C}\)
Vì BC > AC nên \(\widehat{A}>\widehat{B}\) (đối diện cạnh lớn hơn là góc lớn hơn)
Vậy \(\widehat{A}=\widehat{C}>\widehat{B}\)
Đúng 0
Bình luận (0)
Định lý 1
Trong một tam giác, góc đối diện với cạnh lớn hơn thi lớn hơn
=>> Trong tam giác ABC: AB > AC <=> Cˆ>Bˆ
.... gợi ý thoy
hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


















