Trên hình ta có hai đường tròn (A;3cm ) và (B ; 2cm) cắt nhau tại C,D . AB=4cm. Đường tròn tâm A, B lần lượt cắt đoạn thẳng AB tại K,I
a. Tính CA ,CB, DA, DB
b. I có phải là trung điểm của đoạn thẳng AB không?
Trên hình 48, ta có hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm C, bán kính 2cm.
b) Vì sao đường tròn (C; 2cm) đi qua O, A?
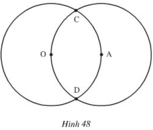
a) Vẽ đường tròn (C; 2cm)
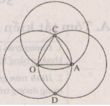
b)
Vì hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C nên:
- C thuộc (O; 2cm) ⇒ OC = 2cm do đó O thuộc (C; 2cm)
- C thuộc (A; 2cm) ⇒ AC = 2cm do đó A thuộc (C; 2cm)
Vậy đường tròn (C; 2cm) đi qua hai điểm O và A.
Trên hình 48, ta có hai đường tròn (0;2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O
a) Vẽ đường tròn tâm C, bán kính 2cm ?
b) Vì sao đường tròn (C; 2cm) đi qua O, A ?
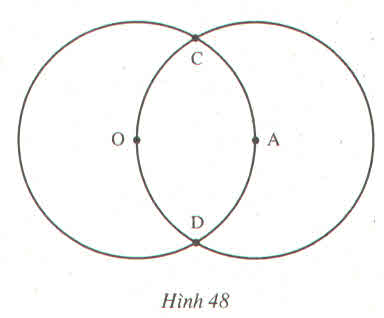
Giải:
a) Xem hình bên
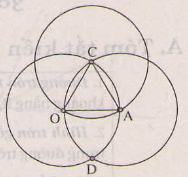
b) Đường tròn (C;2cm) đi qua O và A vì O và A cách C là 2cm.
Câu 59: Trên hình bên, ta có đường tròn (O; R)
A. Điểm O cách mọi điểm trên đường tròn một khoảng R
B. Điểm O cách mọi điểm trên hình tròn một khoảng R
C. Điểm O nằm trên đường tròn
D. Chỉ có câu C đúng
Câu 60: Gọi S1 là diện tích hình tròn bán kính R1 = 1 cm
S2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:
A. S2 = 2S1 B. S2 = S1 C. S2 = 4S1 D. S2 = 3S1
Trên hình vẽ ta có đường tròn tâm O, bán kính 10cm, tứ giác OABC là hình vuông với A và C nằm trên đường tròn. Tìm phần diện tích của hình vuông nằm ngoài đường tròn.
Trên hình 48 , ta có hai đường tròn ( O ; 2 cm ) và ( A ; 2 cm ) cắt nhau tại nhau tại C , D . Điểm A nằm trên đường tròn tâm O
a ) Vẽ đường tròn tâm C , bán kính 2 cm ( ko vẽ cũng được )
b ) Vì sao đường tròn ( C ; 2 cm ) đi qua O và A
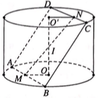
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45 ° . Thể tích của hình trụ bằng:
A. 3 2 π a 3 16
B. π a 3 4
C. 3 2 π a 3 8
D. 2 π a 3 16
Cho một hình trụ tròn xoay và hình vuông (ABCD) cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc . Thể tích của hình trụ bằng
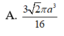
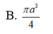
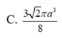

Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
Tập hợp các điểm N thuộc đường tròn (C') là ảnh của (C) qua phép đối xứng qua trung điểm của AB.
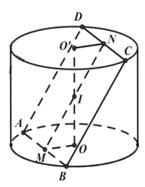
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.
A. πa 3 2 16
B. πa 3 2 4
C. πa 3 2 2
D. 3 πa 3 2 16
Đáp án D
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
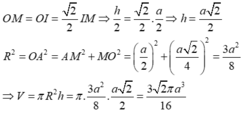
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45 o . Tình thể tích của khối trụ.
A. 3 πa 3 16 .
B . 2 πa 3 16 .
C . πa 3 16 .
D . 3 2 πa 3 16 .