Số nguyên dương x lớn nhất để phân thức A sau đây có giá trị nguyên
\(A=\frac{X^3+X-2}{X^3-3X^2-2X-8}\)
1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị lớn nhất
a. A=1/7-x b.B=27-2x/12-X
2.Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nhỏ nhất
a. A=1/x-3 b. B= 7-x/x-5 c. C= 5x-19/x-4
3.Tìm giá trị nhỏ nhất của các biếu thức sau
a. A=x^4+3x^2 +2 b. B=(x^4+5)^2 c. C=(x-1)^2+(y+2)^2
4.Tìm giá trị lớn nhất của các biểu thức sau
a. A=5-3(2x-1)^2 b.B=1/2(x-1)^2+3 c. C=x^2+8/x^2+2
số nguyên dương x lớn nhat de A=\(\frac{x^3+x-2}{x^3-3x^2-2x-8}\)đạt giá trị nguyên là
A đạt giá trị nguyên là 2 khi x=7
k cho mình nha bạn
Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
a) \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
a) \(A=\dfrac{2x^3-6x^2+x-8}{x-3}\)
Bài 1 : Tìm giá trị của m để PT
\(3-m=\frac{10}{x+2}\)
có nghiệm là số dương
Bài 2 : Cho A=\(\frac{4x-4}{1-2x+x^2}\)
Tìm x để A <0
Bài 3 : Tìm giá trị nguyên của x để giá trị của biểu thức sau là số nguyên:
A=\(\frac{2x^3-6x^2+x-8}{x-3}\)
B= \(\frac{3x^2-x+3}{3x+2}\)
\(3-m=\frac{10}{x+2}\)
\(\Leftrightarrow\left(3-m\right)\left(x+2\right)=10\)
=> 3-m và x+2 thuộc Ư (10)={1;2;5;10}
TH1: \(\hept{\begin{cases}3-m=1\\x+2=10\end{cases}\Leftrightarrow\hept{\begin{cases}m=2\\x=8\end{cases}}}\)hoặc \(\hept{\begin{cases}3-m=10\\x+2=1\end{cases}\Leftrightarrow\hept{\begin{cases}m=-7\\x=1\end{cases}}}\)
TH2: \(\hept{\begin{cases}3-m=5\\x+2=2\end{cases}\Leftrightarrow\hept{\begin{cases}m=-2\\x=0\end{cases}}}\)hoặc \(\hept{\begin{cases}3-m=2\\x+2=5\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\x=-3\end{cases}}}\)(loại)
bài 3:
\(A=\frac{2x^3-6x^2+x-8}{x-3}\left(x\ne3\right)\)
\(\Leftrightarrow A=\frac{\left(2x^3-6x^2\right)+\left(x-8\right)}{x-3}=\frac{2x\left(x-3\right)+\left(x-8\right)}{x-3}=2x+\frac{x-8}{x-3}\)
Để A nguyên thì \(\frac{x-8}{x-3}\)nguyên
Có: \(\frac{x-8}{x-3}=\frac{x-3-5}{x-3}=1-\frac{5}{x-3}\)
Vì x nguyên => x-3 nguyên => x-3 \(\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Ta có bảng
| x-3 | -5 | -1 | 1 | 5 |
| x | -2 | 2 | 4 | 8 |
Tìm số nguyên của x để mỗi phân thức sau có giá trị là số nguyên:
a) (x^4 - 2x^3 - 3x^2 + 8x - 1) / (x^2 - 2x +1)
b) (x^4 + 3x^3 +2x^2 + 6x -2) / (x^2 + 2)
MK ko biế đúng ko nữa , sai thì ý kiến
a)
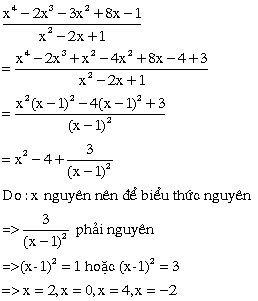
b)
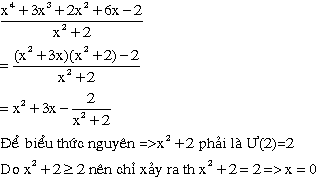
Chúc các bn hok tốt
Tham khảo nhé
Tìm các giá trị nguyên của x để phân thức sau có giá trị 1 số nguyên:
a, \(\frac{3x^3-4x^2+x-1}{x-4}\)
b,\(\frac{3x^2-x+3}{3x+2}\)
c, \(\frac{2x^3-6x^2+x-8}{x-3}\)
d,\(\frac{x^4-16}{x^4-4x^3+8x^2-16x+16}\)
Tìm các gia trị nguyên của x để phân thức sau có giá trị là số nguyên:
A=\(\frac{2x^3-6x^2+x-8}{x-3}\)
tìm giá trị nguyên của x để phân thức sau là số nguyên:
\(A=\frac{x^4+3x^3+2x^2+6x-2}{x^2+2}\)
\(A=\frac{\left(x^4+4x^2+4\right)+\left(3x^3+6x\right)-\left(2x^2+4\right)-2}{x^2+2}\)
\(A=\frac{\left(x^2+2\right)^2+3x\left(x^2+2\right)-2\left(x^2+2\right)-2}{x^2+2}\)
\(A=\frac{\left(x^2+2\right)\left(x^2+3x\right)}{x^2+2}-\frac{2}{x^2+2}=x^2+3x-\frac{2}{x^2+2}\)
Để A là số nguyên, mà x là số nguyên nên \(x^2+3x\)nguyên, do đó \(\frac{2}{x^2+2}\inℤ\)
Do \(x^2+2\ge2\) nên \(x^2+2=2\Leftrightarrow x=0\)