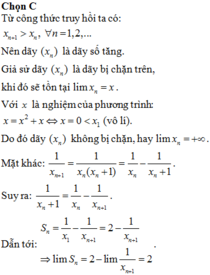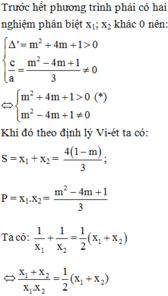1+1:1x1+1-1:1x2

Những câu hỏi liên quan
1+1x2+1x0+1x1=?
Xem thêm câu trả lời
1x1+2=?
Vậy 1x2+1
Xem thêm câu trả lời
1+1x2=?
vậy: 1x1+2 bằng mấy?
Xem thêm câu trả lời
Cho dãy số
x
n
xác định bởi
x
1
1
2
,
x
n
+
1
x
n
2
+
x
n
,
∀
n
≥
1
. Đặt...
Đọc tiếp
Cho dãy số x n xác định bởi
x 1 = 1 2 , x n + 1 = x n 2 + x n , ∀ n ≥ 1 .
Đặt S n = 1 x 1 + 1 + 1 x 2 + 1 + . . . + 1 x n + 1 .
Tính lim S n .
A. + ∞ .
B. - ∞ .
C. 2.
D. 2.
Biết phương trình
x
2
-
3
x
+
1
0
có hai nghiệm
x
1
và
x
2
.
1
x
1
+
1
x
2
bằng: A.
1
3
B.
-...
Đọc tiếp
Biết phương trình x 2 - 3 x + 1 = 0 có hai nghiệm x 1 và x 2 . 1 x 1 + 1 x 2 bằng:
A. 1 3
B. - 1 3
C. 3
D.một kết quả khác
Áp dụng định lí vi- et ta có: x 1 + x 2 = 3 x 1 . x 2 = 1
Ta có: 1 x 1 + 1 x 2 = x 1 + x 2 x 1 . x 2 = 3 1 = 3 .
Đúng 0
Bình luận (0)
Tìm m để phương trình 3
x
2
+ 4(m – 1)x +
m
2
– 4m + 1 0 có hai nghiệm phân biệt
x
1
;
x
2
thỏa mãn:
1
x
1
+
1
x
2
2
x...
Đọc tiếp
Tìm m để phương trình 3 x 2 + 4(m – 1)x + m 2 – 4m + 1 = 0 có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn: 1 x 1 + 1 x 2 = 2 x 1 + x 2
A. m = 1; m = 5
B. m = 1; m = −1
C. m = 5
D. m ≠ 1
Với giá trị nào của m, hàm số
y
x
3
+
2
(
m
-
1
)
x
2
+
(
m
2
-
4
m
+
1
)
x
+
2
(
m
2
+
1
)
có hai điểm cực trị
x
1...
Đọc tiếp
Với giá trị nào của m, hàm số y = x 3 + 2 ( m - 1 ) x 2 + ( m 2 - 4 m + 1 ) x + 2 ( m 2 + 1 ) có hai điểm cực trị x 1 , x 2 thỏa mãn 1 x 1 + 1 x 2 = x 1 + x 2 2
A. m = 5 hoặc m = 1
B. m = 2 hoặc m = 1
C. m = 5
D. m = 1
Chọn A
Ta có y ' = 3 x 2 + 4 ( m - 1 ) x + m 2 - 4 m + 1 . Hàm số có hai cực trị
=> y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> 4 ( m - 1 ) 2 - 3 ( m 2 - 4 m + 1 ) > 0
<=> m 2 + 4 m + 1 > 0
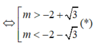
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt x 1 , x 2 ta có
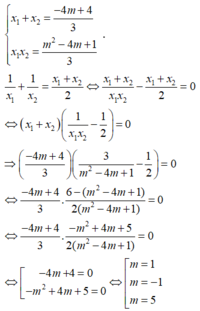
Đối chiếu điều kiện (*) có m = 5 hoặc m = 1
Đúng 0
Bình luận (0)
Cho phương trình bậc hai: x 2 – 5x – 2 = 0. Không giải phương trình để tìm 2 nghiệmx1 ; x2 . Hãy tính giá trị của biểu thức: A =x1−1x2−1+x2−1x1−1
ghi rõ hơn đi ghi như vầy khó hiểu
Đúng 0
Bình luận (0)
Gọi x1; x2 là nghiệm của phương trình
−
2
x
2
−
6
x
−
1
0
. Không giải phương trình, tính giá trị của biểu thức
N
1
x
1
+
3
+
1
x
2
+...
Đọc tiếp
Gọi x1; x2 là nghiệm của phương trình − 2 x 2 − 6 x − 1 = 0 . Không giải phương trình, tính giá trị của biểu thức N = 1 x 1 + 3 + 1 x 2 + 3
A. 6
B. 2
C. 5
D. 4
Phương trình −2 x 2 − 6x − 1 = 0 có = ( − 6 ) 2 – 4.(− 2).(−1) = 28 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = − 3 x 1 . x 2 = 1 2
Ta có
N = 1 x 1 + 3 + 1 x 2 + 3 = x 1 + x 2 + 6 x 1 . x 2 + 3 x 1 + x 2 + 9 = − 3 + 6 1 2 + 3. − 3 + 9 = 6
Đáp án: A
Đúng 0
Bình luận (0)