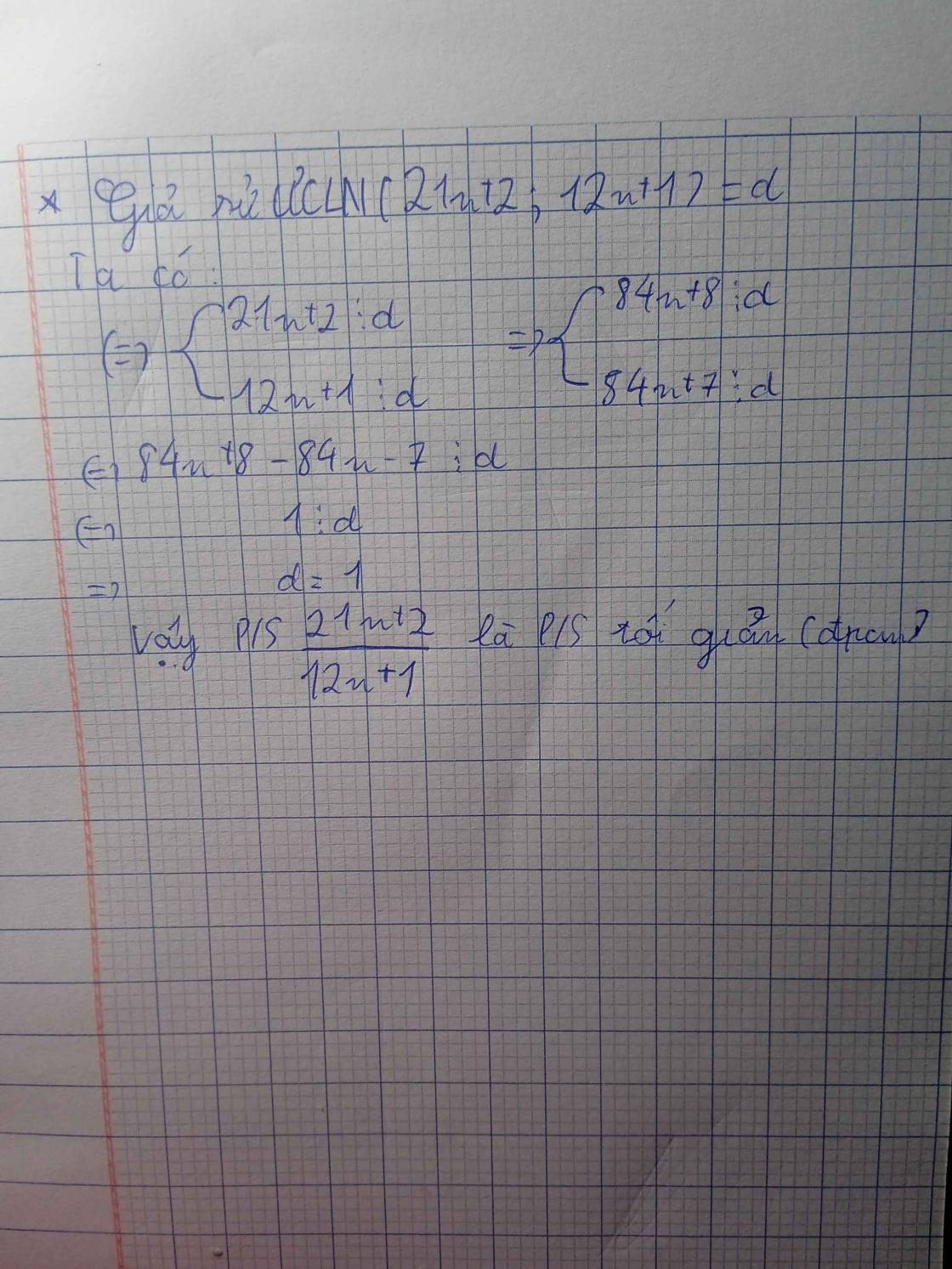tìm số tự nhiên n để phân số 12n+5/ 9n+3 không phải là phân số tối giản

Những câu hỏi liên quan
Với mọi số tự nhiên n,hãy chứng minh các phân số sau đây là phân số tối giản
c.7n+4/9n+5
a.2n+1/4n+3.
b.4n+1/12n+7
Nhớ trả lời nhanh nha
Chứng minh rằng mọi số tự nhiên n, các phân số sau là các phân số tối giản
a) A=2n+1/4n+3. B=14n+1/12n+7. C=7n+4/9n+5
B, ,Tìm tất cả các số tự nhiên n để phân số \(\dfrac{7n+6}{6n+7}\) không phải là phân số tối giản
Tìm số tự nhiên n để\(\frac{2n-1}{9n+4}\)là phân số tối giản
Đặt d là ước nguyên tố của 2n - 1 và 9n + 4
=> 2n - 1 chia hết cho d ; 9n + 4 chia hết cho d
2n - 1 chia hết cho d => 9( 2n - 1 ) chia hết cho d => 18n - 9 chia hết cho d
9n + 4 chia hết cho d => 2( 9n + 4 ) chia hết cho d => 18n + 8 chia hết cho d
=>( 18n + 8 ) - ( 18n - 9 ) chia hết cho d
=>18n + 8 - 18n + 9 chia hết cho d
=> 17 chia hết cho d => d thuộc ước của 17 mà ước của 17 là 1;17
Đúng 0
Bình luận (0)
1) tìm n sao cho phân số tối giản:
12n+1 / 30n+2
2) cho phân số:
n+19/n+6 ( n E N )
a) tìm giá trị n sao cho phân số có giá trị là số tự nhiên
b) tìm giá trị của n để phân số tối giản
a) Chứng minh rằng với mọi số tự nhiên n thì phân số 21n+4/14n+3 là phân số tối giản
b) Tìm tất cả các số tự nhiên n để phân số n+3/n-12 là phân số tối giản
c) Tìm các số tự nhiên n để phân số 21n+3/6n+4 rút gọn được
a) Để 21n+4/14n+3 là phân số tổi giản thì ƯCLN(21n+4; 14n+3) =1
Gọi ƯCLN(21n+4; 14n+3) =d => 21n+4 \(⋮\)d; 14n+3 \(⋮\)d
=> (14n+3) -(21n+4) \(⋮\)d
=> 3(14n+3) -2(21n+4) \(⋮\)d
=> 42n+9 - 42n -8 \(⋮\)d
=> 1\(⋮\)d
=> 21n+4/14n+3 là phân số tối giản
Vậy...
c) Gọi ƯC(21n+3; 6n+4) =d; 21n+3/6n+4 =A => 21n+3 \(⋮\)d; 6n+4 \(⋮\)d
=> (6n+4) - (21n+3) \(⋮\)d
=> 7(6n+4) - 2(21n+3) \(⋮\)d
=> 42n +28 - 42n -6\(⋮\)d
=> 22 \(⋮\)cho số nguyên tố d
d \(\in\){11;2}
Nếu phân số A rút gọn được cho số nguyên tố d thì d=2 hoặc d=11
Nếu A có thể rút gọn cho 2 thì 6n+4 luôn luôn chia hết cho 2. 21n+3 chia hết cho 2 nếu n là số lẻ
Nếu A có thể rút gọn cho 11 thì 21n+3 \(⋮\)11 => 22n -n +3\(⋮\)11 => n-3 \(⋮\)11 Đảo lại với n=11k+3 thì 21n+3 và 6n+4 chia hết cho 11
Vậy với n là lẻ hoặc n là chẵn mà n=11k+3 thì phân số đó rút gọn được
chứng minh phân số 21n+2/12n+1 là phân số tối giản với mọi số tự nhiên n
Chứng minh rằng với mọi số tự nhiên n, phân số 12n+1/2n(n+2) là phân số tối giản
Vì 12n+1 = 12n +24 - 23 = 12 (n+2) - 23
=> 12n+1 / 2 (n+2) = 12 (n+2) - 23 / 2n (n+2) = 12 (n+2) / 2n (n+2) - 23 / 2n (n+2) = 6 / n - 23 / 2n (n+2)
Ta có: 2n (n+2) chia hết cho 2
=> 2n (n+2) là số chẵn
Mà 23 là số lẻ nên phân số 23 / 2n (n+2) là phân số tối giản
=> 6 / n - 23 / 2n (n+2) là phân số tối giản
Vậy 12n+1 / 2 (n+2) là phân số tối giản
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số tự nhiên n, phân số 12n+1/2n(n+2) là phân số tối giản.
Mọi người ai trả lời giúp mình với ! @_@
Đúng 0
Bình luận (0)
Sau một hồi tìm hiểu thì mình đã có lời giải r, bạn nào chưa bt thì tham khảo nhé !
Vì 12n+1 = 12n +24 - 23 = 12 (n+2) - 23
=> 12n+1 / 2 (n+2) = 12 (n+2) - 23 / 2n (n+2) = 12 (n+2) / 2n (n+2) - 23 / 2n (n+2) = 6 / n - 23 / 2n (n+2)
Ta có: 2n (n+2) chia hết cho 2
=> 2n (n+2) là số chẵn
Mà 23 là số lẻ nên phân số 23 / 2n (n+2) là phân số tối giản
=> 6 / n - 23 / 2n (n+2) là phân số tối giản
Vậy 12n+1 / 2 (n+2) là phân số tối giản
Đúng 1
Bình luận (0)
Quách Dương Hà Anh mình ch bt là bạn giải đúng hay sai nhưng nếu giải thích là số lẻ/ số chẵn là phân số tối giản thì sai nhé.
VD: 3/12 = 1/4.
Phải giải thích là 23 là số nguyên tố => 23 chỉ chia hết cho chính nó và 1.
Mà 23 và 1 là số lẻ, còn 2n(n+2) là số chẵn nên 23 không chia hết cho 2n(n+2) =>....
Đúng 0
Bình luận (0)