Tìm các chữ số m,n,p,q biết: m,np = qm,q : 50

Những câu hỏi liên quan
m,np=qm,q:50.Tìm m,n,p,q
Cho hình chữ nhật ABCD, các điểm M, N, P, Q lần lượt là trung điểm của cạnh AB, BC, CD, DA. Các điểm E, F, G, H lần lượt là trung điểm các cạnh MN, NP, PQ và QM. Tính tỉ số diện tích của hình chữ nhật EFGH và hình chữ nhật ABCD.
Tìm các chữ số \(m;n;p\) ,biết rằng : \(mm\times np=n7p2\).
m,np=q,mq:50
Tìm m,n,p,q
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM. Chứng minh rằng MNPQ là hình chữ nhật.
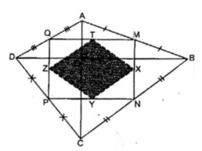
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.
Đúng 0
Bình luận (0)
Giúp mình với ạ!!! Thank nhiều!!!
Cho hình vuông ABCD. Gọi M,N,P,Q là các điểm thuộc các cạnh AB,BC,CD,DA. Biết AB = a
Chứng minh rằng: \(2a^2\le MN^2+NP^2+PQ^2+QM^2\le4a^2\)
Hình vuông ABCD cạnh a có M,N,P,Q thứ tự thuộc các cạnh AB,BC,CD,DA.C/m
2a^2<=MN^2+NP^2+PQ^2+QM^2<=4a^2
Cho hình chữ nhật ABCD, AB = 3, AD = 4. Các điểm M, N, P, Q lần lượt thuộc các cạnh AB, BC, CD, DA. Kí hiệu MN = a, NP = b, PQ = c, QM = d.
Chứng minh : 25 ≤ a2 + b2 + c2 + d2 ≤ 50
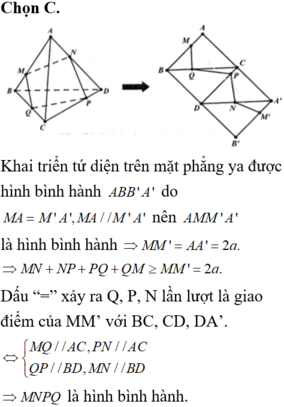
Cho tứ diện đều ABCD cạnh a. Các điểm M, N, P, Q thay đổi tương ứng trên cạnh AB. AD, CD, CB. Giá trị nhỏ nhất của tổng MN + NP + PQ + QM là A. a B.
a
3
C. 2a D. 3a
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Các điểm M, N, P, Q thay đổi tương ứng trên cạnh AB. AD, CD, CB. Giá trị nhỏ nhất của tổng MN + NP + PQ + QM là
A. a
B. a 3
C. 2a
D. 3a