Cho tam giác ABC cân tại A; Góc A =45 độ . Từ trung điểm I của AC kẻ đường thẳng vuông góc với AC cắt BC tại M. Trên tia đối của tia AM lấy N sao cho AN = BM . C/m
a) Góc ANC = góc BAC
b) tam giác ABM = tam giác CAN
c) tam giác MNC vuông cân
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ các tam giác ABD vuông cân tại A, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. CMR: Tứ giác BDEC là hình thang cân
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng tứ giác BDEC là hình thang cân.
tam giác abc cân tại atam giác abc cân tại a cótam giác abc cân tại atam giác abc cân tại a có â40tam giác abc cân tại atam giác abc cân tại a có tam giác abc cân tại atam giác abc cân tại a có â40 khi đó số đo của góc b bằnga,100 độ b,50 độ c, 70 độtam giác abc cân tại atam giác abc cân tại a cótam giác abc cân tại atam giác abc cân tại a có â40tam giác abc cân tại atam giác abc cân tại a có tam giác abc cân tại atam giác abc cân tại a có â40 khi đó số đo của góc b bằng a,100 độ b,50 độ c, 7...
Đọc tiếp
tam giác abc cân tại atam giác abc cân tại a cótam giác abc cân tại atam giác abc cân tại a có â=40tam giác abc cân tại atam giác abc cân tại a có tam giác abc cân tại atam giác abc cân tại a có â=40 khi đó số đo của góc b bằng
a,100 độ b,50 độ c, 70 độtam giác abc cân tại atam giác abc cân tại a cótam giác abc cân tại atam giác abc cân tại a có â=40tam giác abc cân tại atam giác abc cân tại a có tam giác abc cân tại atam giác abc cân tại a có â=40 khi đó số đo của góc b bằng
a,100 độ b,50 độ c, 70 độ d, 40 độ
cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABC vuông cân tại A. Vẽ tam giác ACE vuông cân tại E.C/m rằng BDEC là hình thang cân
Giúp mình với nha!!!!!!!!!!!!!!!!!!!!!
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
1. Cho tam giác ABC cân tại A có góc A 20 độ. Vẽ D trên nửa mặt phẳng bờ AC không chứa B sao cho tam giác BCD cân tại C và góc BCD 140 độ. Tính góc ADC2. Cho tam giác ABC cân tại A có góc BAC 108 độ. D là điểm nằm trong tam giác ABC sao cho góc DBC 12 độ, góc DCB 18 độ. tính góc ADB3. Cho tam giác ABC cân tại A, A 100 độ. M nằm trong tam giác ABC sao cho góc MBC 30 độ, góc MCB 20 độ. Tính góc MAC4. Cho tam giác ABC vuông tại A, vẽ AH vuông góc vs BC tại. Biết BH - HC AC. tính các góc AB...
Đọc tiếp
1. Cho tam giác ABC cân tại A có góc A = 20 độ. Vẽ D trên nửa mặt phẳng bờ AC không chứa B sao cho tam giác BCD cân tại C và góc BCD = 140 độ. Tính góc ADC
2. Cho tam giác ABC cân tại A có góc BAC = 108 độ. D là điểm nằm trong tam giác ABC sao cho góc DBC = 12 độ, góc DCB = 18 độ. tính góc ADB
3. Cho tam giác ABC cân tại A, A = 100 độ. M nằm trong tam giác ABC sao cho góc MBC = 30 độ, góc MCB = 20 độ. Tính góc MAC
4. Cho tam giác ABC vuông tại A, vẽ AH vuông góc vs BC tại. Biết BH - HC = AC. tính các góc ABC, ACB
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?
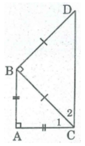
Vì ΔABC vuông cân tại A nên 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A . Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B . Tứ giác ABDC là hình gì? Chứng minh
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Xem thêm câu trả lời
cho tam giác ABC vuông cân tại A . Ở phía ngoài tam giác ABC , vẽ tam giác BCDvuông cân tại B. Tứ giác ABCD là hình gì ? Vì sao ?
Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.
Đúng 0
Bình luận (0)