Cho tam giác ABC đường trung tuyến AD.Lấy điểm O nằm giữa A và D.Qua O vẽ đường thẳng d cắt các tia AB,AC lần lượt tại E và F . Xác định vị trí của O để BE/AE + CF/AF = 1

Những câu hỏi liên quan
Cho tam giác ABC có AD là đường trung tuyến. Lấy điểm O nằm giữa A và D. Qua O vẽ đường thẳng d cắt các tia AB, AC tại E và F. Hãy xác định vị trí của điểm O để BE / AE + CF / AF = 1.
Trường hợp 1: Đường thẳng d song song với BC.
Theo định lý Ta - lét ta có:\(\frac{BE}{EA}=\frac{OD}{OA}\frac{CD}{FA}=\frac{OD}{OA}\)
Suy ra : \(\frac{BE}{AE}+\frac{CF}{AF}=1\Leftrightarrow\frac{OD}{OA}+\frac{OD}{OA}=1\Leftrightarrow2OD=OA\left(1\right)\)
TRƯỜNG HỢP 2 LÀM TƯƠNG TỰ NHA :D
Đúng 0
Bình luận (0)
Cho tam giác ABC , đường trung tuyến AD . Lấy điểm O nằm giữa A và D . Qua O lấy đường thằng d cắt tia AB , AC tại E và F . Hãy xác định vị trí của điểm O để \(\frac{BE}{AE}+\frac{CF}{AF}=1\)
Bạn tham khảo tại đây
https://olm.vn/hoi-dap/detail/97829537475.html
Cho tam giác ABC có AD là đường trung tuyến. Lấy điểm O nằm giữa A và D. Qua O vẽ đường thẳng d cắt các tia AB, AC tại E và F. Hãy xác định vị trí của điểm O để BE / AE + CF / AF = 1.
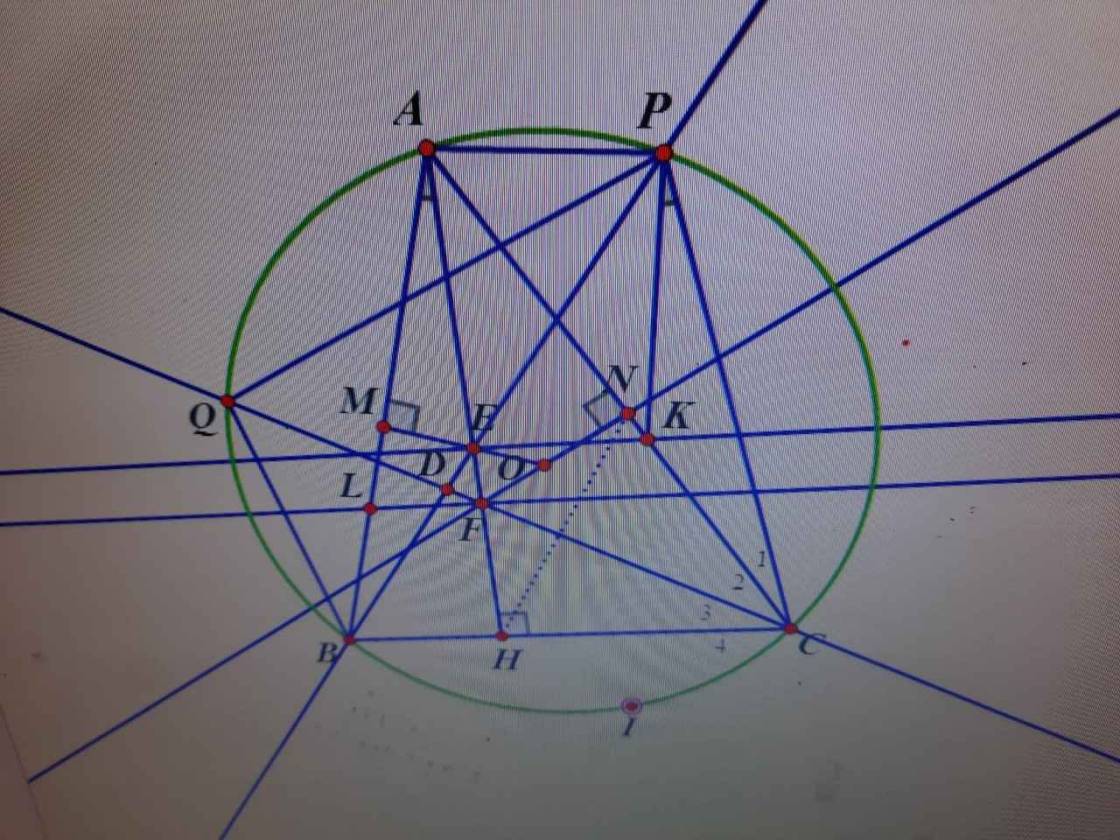
cho tam giác nhọn ABC (AB AC) nội tiếp đường tròn tâm O, các điểm M, N lần lượt là trung điểm của AB, AC. Đường cao kẻ từ A của tam giác ABC cắt OM, ON lần lượt tại các điểm E, F. đường thẳng BE, CF cắt nhau tại D. Tia BE, CF cắt (O) lần lượt tại P, Q. lấy điểm K trên AC, L trên BA sao cho EK//LF//BC.a) chứng minh 4 điểm A,P, E, K nằm trên 1 đường tròn. b) PQBC là hình thang cân.c) chứng minh K, L nằm trên phân giác ngoài của góc BDC
Đọc tiếp
cho tam giác nhọn ABC (AB <AC) nội tiếp đường tròn tâm O, các điểm M, N lần lượt là trung điểm của AB, AC. Đường cao kẻ từ A của tam giác ABC cắt OM, ON lần lượt tại các điểm E, F. đường thẳng BE, CF cắt nhau tại D. Tia BE, CF cắt (O) lần lượt tại P, Q. lấy điểm K trên AC, L trên BA sao cho EK//LF//BC.a) chứng minh 4 điểm A,P, E, K nằm trên 1 đường tròn. b) PQBC là hình thang cân.c) chứng minh K, L nằm trên phân giác ngoài của góc BDC
a: EN//BC
=>góc ANE=góc ACB=góc APB
=>APEK nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Lấy C thuộc tia đối của tia BA, vẽ đường thẳng d vuông góc với AB tại C. Gọi I là trung điểm OB, E là điểm thuộc đường tròn (O) tại F. Các đường thẳng AE, AF cắt đường thẳng d lần lượt tại K và D
1) cm CBEK là tứ giác nội tiếp
2)cm AE.AK=AF.AD
3)Xác định vị trí điểm E để OEBF là hình thoi
cho (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB.Tiếp tuyến tại A của (O) cắt các đường thẳng BC và BD lần lượt tại E và F.Gọi P và Q lần lượt là trung điểm của AE và AF.
1.Gọi H là trực tâm của tam giác BPQ.chứng min H là trung điểm của OA.
2.Xác định vị trí của CD để tam giác BPQ có diện tích nhỏ nhất
Cho tam giác ABC , trung tuyến AD , O là trọng tâm của tam giác . Qua O vẽ đường thẳng d cắt các tia AB , AC tại E và F .
Chứng minh rằng : \(\frac{BE}{AE}\) + \(\frac{CF}{AF}\) = 1
Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AD,AE (D,E là các tiếp điểm).Vẽ các tuyến ABC của đường tròn (O) sao cho điểm B nằm giữa hai điểm A và C; tia AC nằm giữa hai tia AD và AO.Từ điểm O kẻ OI vuông góc AC tại Ia.C/m năm điểm A,D,I,O,E cùng nằm trên một đường trònb.C/m IA là tia phân giác của DIE và AB.ACAD^2c.Gọi K và F lần lượt là giao điểm của ED với AC và OI. Qua điểm D vẽ đường thẳng ssong với IE cắt Ò và AC lần lượt tại H và P.C/m D là trung điểm của HP
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AD,AE (D,E là các tiếp điểm).Vẽ các tuyến ABC của đường tròn (O) sao cho điểm B nằm giữa hai điểm A và C; tia AC nằm giữa hai tia AD và AO.Từ điểm O kẻ OI vuông góc AC tại I
a.C/m năm điểm A,D,I,O,E cùng nằm trên một đường tròn
b.C/m IA là tia phân giác của DIE và AB.AC=AD^2
c.Gọi K và F lần lượt là giao điểm của ED với AC và OI. Qua điểm D vẽ đường thẳng ssong với IE cắt Ò và AC lần lượt tại H và P.C/m D là trung điểm của HP
Cho đường tròn (O;R) và từ một điểm A ở bên ngoài, ta vẽ hai tiếp tuyến AB và AC với đường tròn. Gọi M là trung điểm AB.Tia CM cắt đường tròn tại điểm N.Tia AN cắt đường tròn tại điểm D.a) Chứng minh tứ giác ABOC nội tiếpb) Chứng minh MB2 MC.MN ; AB//CDc) Giả sử OA 2R.Chứng minh tứ giác ABDC là hình thoi.d) Vẽ cát tuyến AEF (E,F (O); E nằm giữa A và F). Xác định vị trí của cát tuyến AEF để AE + AF lớn nhất.
Đọc tiếp
Cho đường tròn (O;R) và từ một điểm A ở bên ngoài, ta vẽ hai tiếp tuyến AB và AC với đường tròn. Gọi M là trung điểm AB.Tia CM cắt đường tròn tại điểm N.Tia AN cắt đường tròn tại điểm D.
a) Chứng minh tứ giác ABOC nội tiếp
b) Chứng minh MB2 = MC.MN ; AB//CD
c) Giả sử OA = 2R.Chứng minh tứ giác ABDC là hình thoi.
d) Vẽ cát tuyến AEF (E,F (O); E nằm giữa A và F). Xác định vị trí của cát tuyến AEF để AE + AF lớn nhất.