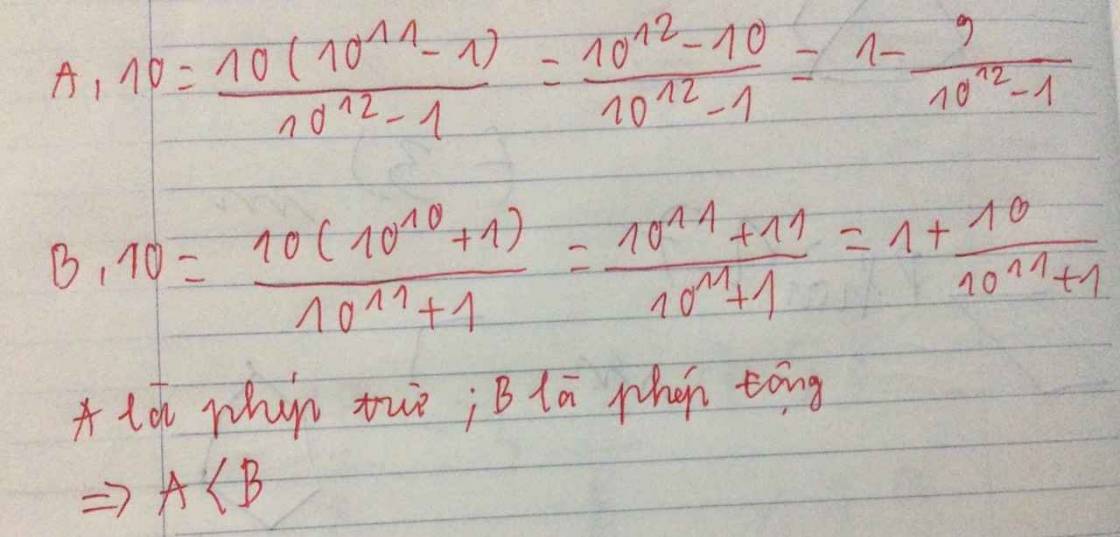2)Ta có: \(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)

              \(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)

Vì \(8^{111}< 9^{111}\) mà \(2^{332}< 8^{111},3^{223}>9^{111}\) nên suy ra \(2^{332}< 3^{223}\)

Vậy \(2^{332}< 3^{223}\)

1) \(A=\dfrac{10^{2013}+1}{10^{2014}+1}\Rightarrow10A=\dfrac{10^{2014}+10}{10^{2014}+1}=\dfrac{10^{2014}+1}{10^{2014}+1}+\dfrac{9}{10^{2014}+1}=1+\dfrac{9}{10^{2014}+1}\)

\(B=\dfrac{10^{2014}+1}{10^{2015}+1}\Rightarrow10B=\dfrac{10^{2015}+10}{10^{2015}+1}=\dfrac{10^{2015}+1}{10^{2015}+1}+\dfrac{9}{10^{2015}+1}=1+\dfrac{9}{10^{2015}+1}\)Vì: \(10^{2014}+1< 10^{2015}+1\Rightarrow\dfrac{9}{10^{2014}+1}>\dfrac{9}{10^{2015}+1}\Rightarrow1+\dfrac{9}{10^{2014}+1}>1+\dfrac{9}{10^{2015}+1}\)

Nên suy ra \(10A>10B\Rightarrow A>B\)

a,\(A=\frac{1}{5}+\frac{1}{5^2}+\frac{1}{5^3}+...+\frac{1}{5^{100}}\)

\(=>5A=1+\frac{1}{5}+\frac{1}{5^2}+...+\frac{1}{5^{99}}\)

\(=>5A-A=1-\frac{1}{5^{100}}=>A=\frac{1-\frac{1}{5^{100}}}{4}\)

b, Ta có \(1-\frac{1}{5^{100}}< 1=>\frac{1-\frac{1}{5^{100}}}{4}< \frac{1}{4}\)hay \(A< \frac{1}{4}\)

Lời giải:

a) Xét hiệu \(\frac{a+n}{b+n}-\frac{a}{b}=\frac{(a+n).b-a(b+n)}{b(b+n)}=\frac{n(b-a)}{b(b+n)}\)

Nếu $b>a$ thì $\frac{a+n}{b+n}-\frac{a}{b}>0\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$

Nếu $b<a$ thì $\frac{a+n}{b+n}-\frac{a}{b}<0\Rightarrow \frac{a+n}{b+n}<\frac{a}{b}$

Nếu $b=a$ thì $\frac{a+n}{b+n}-\frac{a}{b}=0\Rightarrow \frac{a+n}{b+n}=\frac{a}{b}$

b) Rõ ràng $10^{11}-1< 10^{12}-1$. 

Đặt $10^{11}-1=a; 10^{12}-1=b; 11=n$ thì: $a< b$; $A=\frac{a}{b}$ và $B=\frac{10^{11}+10}{10^{12}+10}=\frac{a+n}{b+n}$

Áp dụng kết quả phần a:

$b>a\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$ hay $B>A$

Có : 10A = 10.(10^11-1)/10^12-1 = 10^12-10/10^12-1 

Vì : 0 < 10^12-10 < 10^12-1 => 10A < 1 (1)

10B = 10.(10^10+1)/10^11+1 = 10^11+10/10^11+1

Vì : 10^11+10 > 10^11+1 > 0 => 10B > 1 (2)

Từ (1) và (2) => 10A < 10B

=> A < B

Tk mk nha

\(A=\frac{10^{11}-1}{10^{12}-1}\)

\(B=\frac{10^{10}+1}{10^{11}+1}\)

Mà \(\frac{10^{11}-1}{10^{12}-1}< 1\); \(\frac{10^{10}+1}{10^{11}+1}< 1\)

\(\Rightarrow\)\(A,B< 1\)

Ta có:

\(10^{11}-1>10^{10}+1\); \(10^{12}-1>10^{11}+1\)

\(\Rightarrow A>B\)

Vậy A > B

Có : 10A = 10^12-10/10^12-1 = 1 - 9/10^12-1 < 1

10B = 10^11+10/10^11+1 = 1 + 9/10^11+1 > 1

=> 10A < 10B

=> A < B

Tk mk nha

=935 nhe bé

\(A=\dfrac{10^{11}+1}{10^{12}-1}\)

\(\Rightarrow10A=\dfrac{10^{11}+1}{10^{12}-1}.10\)

\(\Rightarrow10A=\dfrac{10\left(10^{11}+1\right)}{10^{12}-1}\)

\(\Rightarrow10A=\dfrac{10^{12}-10}{10^{12}-1}\)

\(B=\dfrac{10^{10}+1}{10^{11}+1}\)

\(\Rightarrow10B=\dfrac{10^{10}+1}{10^{11}+1}.10\)

\(\Rightarrow10B=\dfrac{\left(10^{10}+1\right).10}{10^{11}+1}\)

\(\Rightarrow10B=\dfrac{10^{11}+10}{10^{11}+1}\)

Ta thấy:

 \(10^{12}-1>10^{12}-10>0\Rightarrow10A< 1\)

\(0< 10^{11}+1< 10^{11}+10\Rightarrow10B>1\)

Mà \(10A< 1;10B>1\)

\(\Rightarrow B>A\).

Bạn tham khảo cách giải này ạ: 

Nếu có 1  phân số \(\dfrac{a}{b}\) < 1 thì a/b < a+n/b+n.

Tương tự ta có: A <   (1011 -1)+11/(1012-1)+10

                        A < 1011+10/1012+10

                        A < 10(1010+1)/10(1011+1)

                        A < 10(1010+1)/10(1011+1)

                        A < 1010+1/1011+1

Vậy A< B ( đcpcm )

bai toan nay kho