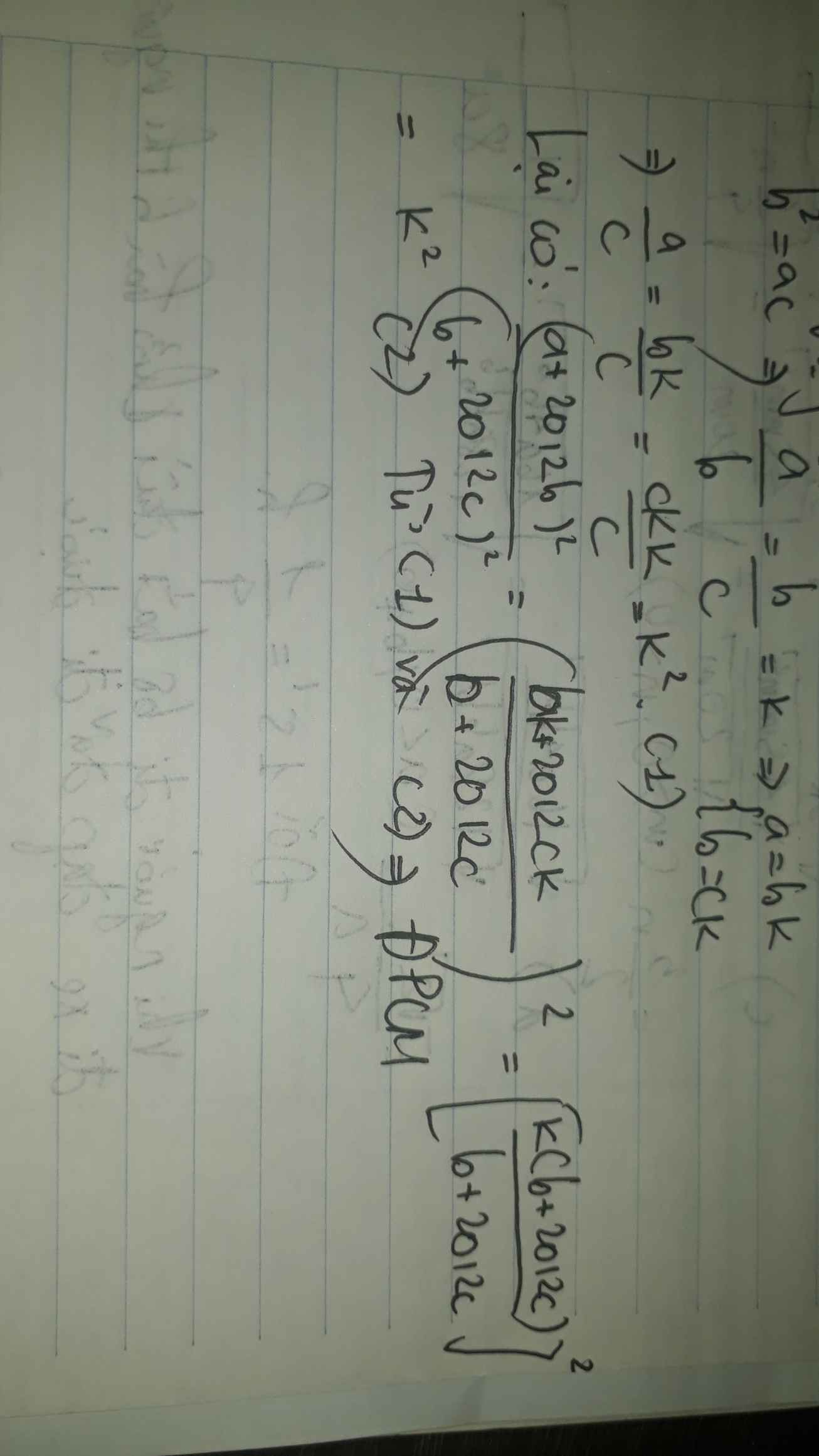Cho a,b,c khác 0 và đooi một khác nhau thoả mãn b+c/b.c=2/a. Chứng minh b/c=a-b/c-a

Những câu hỏi liên quan
Cho a,b,c khác 0 và đôi một khác nhau thỏa mãn:
\(\frac{b+c}{b.c}=\frac{2}{a}\)Chứng minh : \(\frac{b}{c}=\frac{a-b}{c-a}\)
cho ba số khác nhau từng đôi một và khác 0 thoả mãn : a/b+c = b/a+c = c/a+b Chứng minh :
A = b+c/a + a+c/b + a+b/c không phụ thuộc vào các giá trị của a, b, c
\(\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}\) => \(\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=\frac{\left(b+c\right)+\left(a+c\right)+\left(a+b\right)}{a+b+c}=2\)
=> A = 2 + 2+ 2 = 6
vậy...
Đúng 0
Bình luận (0)
\(\text{Giải :}\)
\(\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}\)
\(\Rightarrow\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=\frac{\left(b+c\right)+\left(a+c\right)+\left(a+b\right)}{a+b+c}=2\)
\(\Rightarrow\text{A = 2 + 2 + 2 = 2 . 3 = 6}\)
\(\text{Vậy ....................}\)
\(\text{Giải :}\)
\(\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}\)
\(\Rightarrow\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=\frac{\left(b+c\right)+\left(a+c\right)+\left(a+b\right)}{a+b+c}=2\)
\(\Rightarrow\text{A = 2 + 2 + 2 = 2 . 3 = 6}\)
\(\text{#Hok tốt!}\)
: Cho a,b,c thuộc R và a,b,c khác 0 thoả mãn b2 = ac. Chứng minh rằng:
a/c=(a+2012b)^2/(b+2012c)2
Cho các số a,b,c đoi một khác nhau và khác 0 thoả mãn \(a+\frac{1}{b}=b+\frac{1}{b}\)Chứng minh rằng |abc|=1
Chứng minh rằng : nếu a,b,c là 3 số khác nhau thoả mãn a^3+b^3+c^3=3abc thì a+b+c=0
Ta có a3 + b3 + c3 = 3abc
<=> (a + b)3 - 3ab(a + b) + c3 = 3abc
<=> (a + b + c)[(a + b)2 - (a + b)c + c2] - 3ab(a + b + c) = 0
<=> (a + b + c)(a2 + 2ab + b2 - ac - bc + c2 - 3ab) = 0
<=> (a + b + c)(a2 + b2 + c2 - ab - ac - bc) = 0
<=> \(\orbr{\begin{cases}a+b+c=0\left(\text{tmđk}\right)\\a^2+b^2+c^2-ab-ac-bc=0\end{cases}}\)
Khi a2 + b2 + c2 - ab - ac - bc = 0
<=> 2a2 + 2b2 + 2c2 - 2ab - 2ac - 2bc = 0
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (a2 - 2ac + c2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
<=> \(\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\Leftrightarrow a=b=c\left(\text{loại}\right)\)
Vậy a + b + c = 0
cho a,b,c khác 0 vá đôi một khác nhau thỏa mãn: (b+c)/(bc)=2/a. Chứng minh b/c=a-b/c-a
1)Cho a,b,c đôi một khác nhau và khác 0,thoả mãn:(a+b)/c=(b+c)/a=(c+a)/b
Tính P=(1+a/b).(1+b/c).(1+c/a)
Câu hỏi của Chu Hoàng THủy Tiên - Toán lớp 7 - Học toán với OnlineMath
Cho ba số thực a,b,c khác 0 thoả mãn a(1/b+1/c)+ b(1/c+1/a)+ c(1/a+1/c)= -2. Chứng minh rằng (a+b)(b+c)(c+a)=0
Xem thêm câu trả lời
(Chuyên Toán HN 2016) Cho các số thực a, b, c đôi một khác nhau thỏa mãn a^3 + b^3 + c^3 = 3abc và abc khác 0. Tính giá trị của biểu thức: P = a.b^2/(a^2 + b^2 - c^2) + b.c^2/(b^2 + c^2 - a^2) + c.a^2/(c^2 + a^2 - b^2)
từ a^3 + b^3 + c^3 =3abc => a+b+c = 0
=> a+b= -c <=> c^2 = (a+b)^2
tương tự với -b và -a
=> P = ab^2/a^2+b^2-a^2-2ab-b^2 + bc^2/b^2+c^2-b^2-2bc-c^2 + ca^2/c^2 + a^2 - c^2-2ac-a^2
= -a/2 - b/2 - c/2 = -1/2(a+b+c)=0
Đúng 1
Bình luận (0)