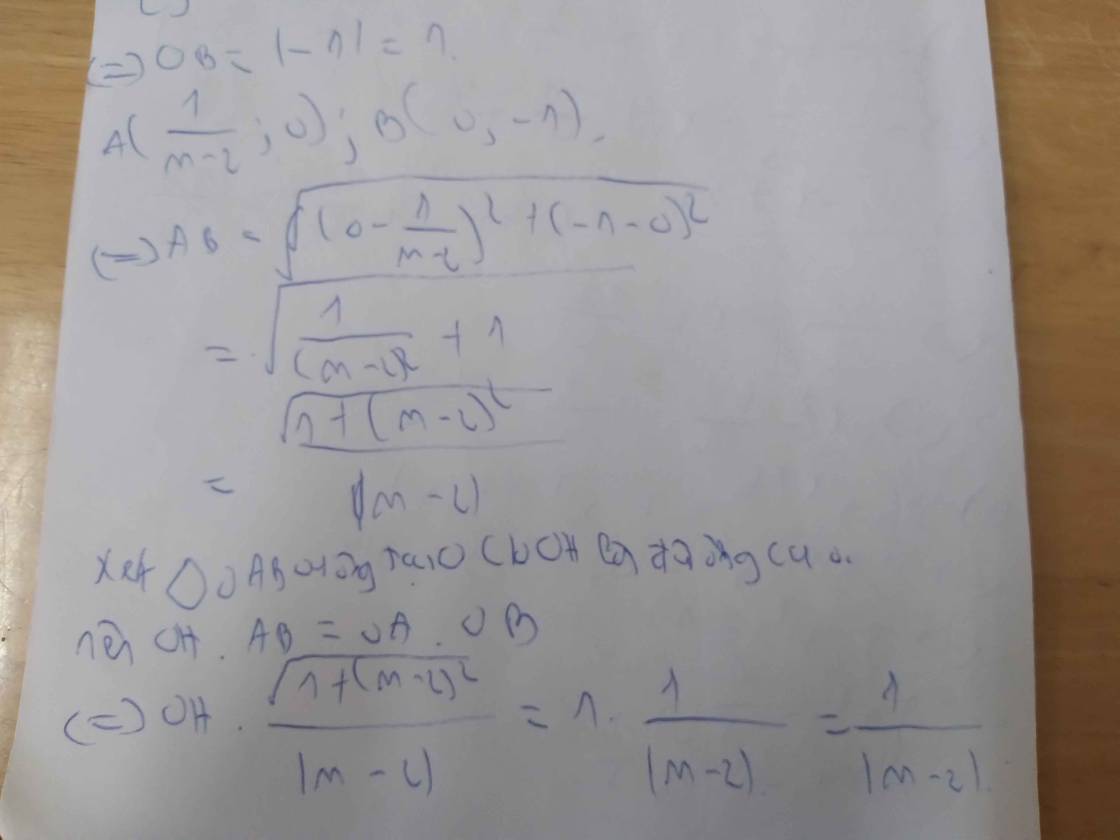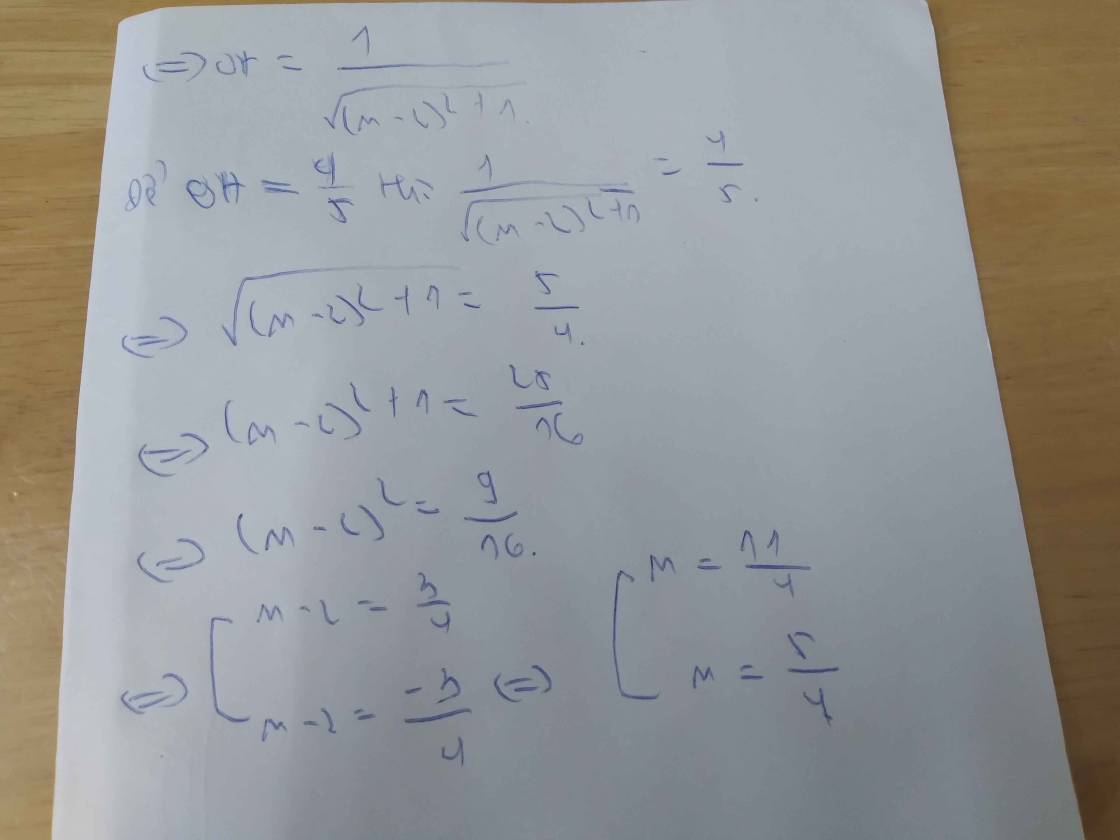y=(m-1).x +4 (d)/ tìm m sao cho khoảng cách từ gốc tọa độ đến( d )bằng 2

Những câu hỏi liên quan
Cho (d) y=mx+2
a, Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1
b, Tìm m để khoảng cách từ gốc tọa độ đến (d) lớn nhất
Giải nhanh nhanh giúp mình với nhaaaa:(
Ta có :
y = m\(x\) + 2
⇒ y - m\(x\) - 2 = 0
⇒ -m\(x\) + y - 2 = 0
⇒d(O;d) = \(\dfrac{\left|0-0-2\right|}{\sqrt{m^2+1}}\) = 1
⇒ \(\sqrt{1+m^2}\) = 2
⇒ 1 + m2 = 4 ⇒ m2 = 3 ⇒ m = -\(\sqrt{3}\); m = \(\sqrt{3}\)
b, d(O;d) = \(\dfrac{2}{\sqrt{m^2+1}}\)
2 > 0; 1 + m2 > 0 Vậy \(\dfrac{2}{\sqrt{m^2+1}}\) lớn nhất ⇔ 1 + m2 nhỏ nhất.
m2 ≥ 0 ⇒ 1 + m2 ≥ 1 vậy m2 + 1 đạt giá trị nhỏ nhất là 1 khi m = 0
⇒d(max) = 2 ⇒ m= 0
Vậy m = 0 thì khoảng cách từ gốc tọa độ đến đường thẳng d là lớn nhất và khoảng cách đó là 2
Kết luận a, Với m = -\(\sqrt{3}\); \(\sqrt{3}\) thì khoảng cách từ gốc tọa độ tới d bằng 1
b, Với m = 0 thì khoảng cách từ gốc tọa độ tới d bằng 2 là khoảng cách lớn nhất .
Đúng 1
Bình luận (0)
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Bạn viết sai rồi, đường thẳng y-mx+2 =0 hay y=mx+2 vậy bạn?
(d):y=mx+3. Tìm m sao cho khoảng cách từ gốc tọa độ đến (d) bằng 1.
(d): y=mx+3
=>mx-y+3=0
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|m\cdot0+\left(-1\right)\cdot0+3\right|}{\sqrt{m^2+\left(-1\right)^2}}=\dfrac{3}{\sqrt{m^2+1}}\)
Để d(O;(d))=1 thì \(\dfrac{3}{\sqrt{m^2+1}}=1\)
=>\(\sqrt{m^2+1}=3\)
=>\(m^2+1=9\)
=>\(m^2=8\)
=>\(m=\pm2\sqrt{2}\)
Đúng 1
Bình luận (0)
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Tìm M để khoảng cách từ gốc tọa độ đến đường thẳng d: y=(m-2)x-1 bằng 4/5
Cho hàm số y = (m - 1)x + 4 (m≠1) có đồ thị là đường thẳng (d)
a) Tìm m để đồ thị hàm số đi qua điểm A(1; 2)
b) Tìm m sao cho khoảng cách từ gốc tọa độ đến (d) bằng 2
a: Thay x=1 và y=2 vào y=(m-1)x+4, ta được:
1(m-1)+4=2
=>m-1+4=2
=>m+3=2
=>m=-1
b:
(d): y=(m-1)x+4
=>(m-1)x-y+4=0
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m-1\right)^2+1}}=\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}\)
Để d(O;(d))=2 thì \(\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}=2\)
=>\(\sqrt{\left(m-1\right)^2+1}=2\)
=>\(\left(m-1\right)^2+1=4\)
=>\(\left(m-1\right)^2=3\)
=>\(m-1=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+1\)
Đúng 0
Bình luận (0)
\(\left(d\right):y=\left(m-1\right)x+4\) (m tham số)
tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 2
y=(m-1)x+4
=>(m-1)x-y+4=0
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m-1\right)^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}\)
Để d(O;(d))=2 thì \(\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}=2\)
=>\(\sqrt{\left(m-1\right)^2+1}=2\)
=>\(\left(m-1\right)^2+1=4\)
=>\(\left(m-1\right)^2=3\)
=>\(m-1=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+1\)
Đúng 2
Bình luận (0)
cho đường thẳng (d): y=m(2x-1)+3-2x
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng 1.
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) đạt giá trị lớn nhất.