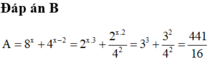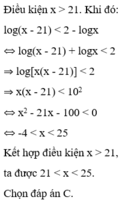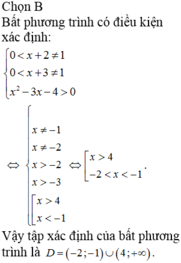tìm x biết: logx 2∛2 = 4

Những câu hỏi liên quan
Cho biết
S
1
x
,
y
log
3
+
x...
Đọc tiếp
Cho biết S 1 = x , y log 3 + x 2 + y 2 ≤ 1 + log x + y S 2 = x , y log 253 + x 2 + y 2 ≤ 2 + log x + y . Tỷ số diện tích S 2 S 1 là
A. 100
B. 101
C. 102
D. 103
Đáp án B
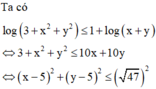
Suy ra S 1 là một hình tròn có bán kính bằng 47 nên diện tích bằng 47 π
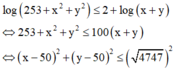
Suy ra S 2 là một hình tròn có bán kình bằng 4747 nên diện tích bằng 4747 π
Tỷ số cần tính là S 2 S 1 = 4747 π 47 π = 101
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a) \(logx+logx^2=log9x\);
b) \(logx^4+log4x=2+logx^3\)
c) \(log^{\left[\left(x+2\right)\left(x+3\right)\right]}_4+log^{\dfrac{x-2}{x+3}}_4=2\)
d) \(log^{\left(x-2\right)log^x_5}_{\sqrt{3}}=2log_3^{\left(x-2\right)}\)
Tìm tập xác định của hàm số
y
log
x
(
x
-
2
)
2
-
1
A. B. C. D.
Đọc tiếp
Tìm tập xác định của hàm số y = log x ( x - 2 ) 2 - 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tập nghiệm của bất phương trình
log
1
2
x
+
5
2
log
x
2
A. (0; 4) B.
(
2
;
4
)
C. (-∞; 1) ∪
(
2
;
4
)
...
Đọc tiếp
Tìm tập nghiệm của bất phương trình log 1 2 x + 5 2 > log x 2
A. (0; 4)
B. ( 2 ; 4 )
C. (-∞; 1) ∪ ( 2 ; 4 )
D. (0; 1) ∪ ( 2 ; 4 )
Điều kiện: x > 0
Ta có:
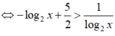
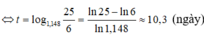
Đặt t = log 2 x , nhận được bất phương trình
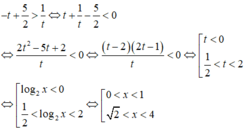
Chọn D
Đúng 0
Bình luận (0)
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
Tìm tập xác định của các hàm số sau: y = logx + log x + 2
logx + log(x + 2) ≥ 0
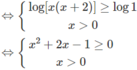
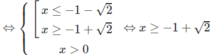
Vậy tập xác định là D = [−1 + 2 ; + ∞ )
Đúng 0
Bình luận (0)
Bất phương trình
l
o
g
x
+
3
(
x
2
-
3
x
-
4
)
≥
l
o
g
x
+
2
(
x
2
-
3
x
-
4
)
có tập xác địn...
Đọc tiếp
Bất phương trình l o g x + 3 ( x 2 - 3 x - 4 ) ≥ l o g x + 2 ( x 2 - 3 x - 4 ) có tập xác định D bằng
![]()
![]()
![]()
![]()
Bất phương trình
log
x
+
3
(
x
2
-
3
x
-
4
)
≥
log
x
+
2
(
x
2
-
3
x
-
4
)
có tập xác định D bằng
A
.
...
Đọc tiếp
Bất phương trình log x + 3 ( x 2 - 3 x - 4 ) ≥ log x + 2 ( x 2 - 3 x - 4 ) có tập xác định D bằng
A . ( - 1 ; 4 )
B . ( - 2 ; - 1 ) ∪ ( 4 ; + ∞ )
C . ( - 2 ; - 4 )
D . ( - 4 ; 1 ) ∪ ( 2 ; + ∞ )
Chọn B
Bất phương trình có điều kiện xác định:
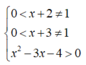
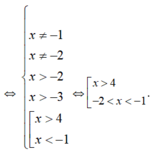
Vậy tập xác định của bất phương trình là ![]()
Đúng 0
Bình luận (0)
Bất phương trình
log
x
+
3
(
x
2
-
3
x
-
4
)
≥
log
x
+
2
(
x
2
-
3
x
-
4
)
có tập xác định D bằng A. (-1; 4) B.
(...
Đọc tiếp
Bất phương trình log x + 3 ( x 2 - 3 x - 4 ) ≥ log x + 2 ( x 2 - 3 x - 4 ) có tập xác định D bằng
A. (-1; 4)
B. ( - 2 ; - 1 ) ∪ ( 4 ; + ∞ )
C. ( - 2 ; 4 )
D. ( - 4 ; 1 ) ∪ ( 2 ; + ∞ )
Biết rằng phương trình
log
2
x
-
15
.
log
x
2
2
có hai nghiệm
x
1
,
x
2
x
1
x
2...
Đọc tiếp
Biết rằng phương trình log 2 x - 15 . log x 2 = 2 có hai nghiệm x 1 , x 2 x 1 > x 2 . Giá trị của x 1 - 16 x 2 bằng
A. - 4095 8
B. 34
C. 30
D. 4097 8