Trong hệ trục tọa độ Oxy, lấy các điểm A và B sao cho A(1;1) , B(9;1). Viết phương trình của đường thẳng d vuông góc với AB và chia tam giác OAB thành hai phần có diện tích bằng nhau.

Những câu hỏi liên quan
trong hệ tọa độ Oxy , cho 2 điểm A( 2;2 ) và B( 1;5 ) . tìm tọa độ điểm M trên trục tung sao cho độ dài MA + MB nhỏ nhất
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A(2;1);điểm B nằm trên trục hoành,điểm C nằm trên trục tung sao cho các điểm B,C có tọa độ không âm.Tìm tọa độ các điểm B;C sao cho tam giác ABC có diện tích lớn nhất.
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Theo Cô si 4x+\frac{1}{4x}\ge2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014
Hơn nữa A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right. \Leftrightarrow x=\dfrac{1}{4} .
Vậy GTNN = 2014
trong hệ trục tọa độ Oxy cho điểm A(2;3).Tọa độ của điểm B sao cho trục Ox là đường trung trực của đoạn thẳng AB
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. A. M (1 ; 0) B. M(4; 0) C.
M
−
5
3
;
−
1
3
.
D.
M
17
7
;
0...
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng.
A. M (1 ; 0)
B. M(4; 0)
C. M − 5 3 ; − 1 3 .
D. M 17 7 ; 0 .
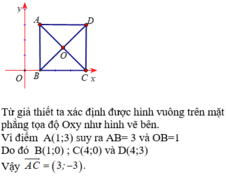
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và
B
C
→
cùng hướng với
i
→
. Tìm tọa độ các vectơ
A
C
→
? A.(1;2) B.(3;4) C.(3;-3) D.(3;0)
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và B C → cùng hướng với i → . Tìm tọa độ các vectơ A C → ?
A.(1;2)
B.(3;4)
C.(3;-3)
D.(3;0)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 điểm A91;2) và B(4;3). Tìm tọa độ điểm M trên trục hoành sao cho góc AMB bằng 45 độ.
Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)
Đúng 2
Bình luận (0)