1/51 + 1/52 + 1/53 + ... + 1/100
Những câu hỏi liên quan
1/51 + 1/52 +1/53 +...+1/100 =?
\(A=\dfrac{1}{51}+\dfrac{1}{52}+\dfrac{1}{53}+...+\dfrac{1}{100}\)
Tham khảo: (mk chx chắc lắm đâu nha)
Đúng 0
Bình luận (0)
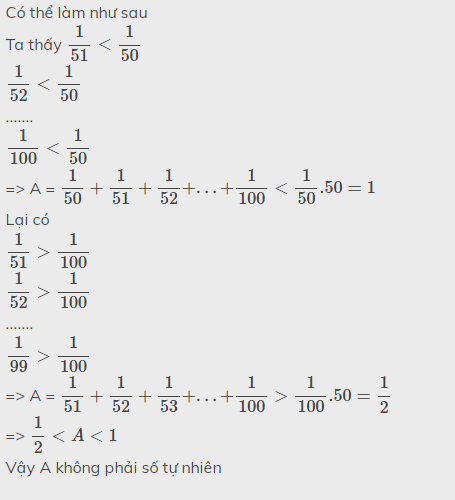
Tính tổng 1/51+1/52+1/53+...+1/99+1/100
Ta có:\(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-\left(1+\frac{1}{2}+...+\frac{1}{50}\right)=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}\)
Đúng 4
Bình luận (0)
@Ác Mộng ở đoạn cuối tự nhiên bỏ mất số 2 luôn, giải sai rồi kìa
Đúng 0
Bình luận (0)
Tính A=1/51+1/52+1/53+...+1/99+1/100
1/51+1/52+1/53+......+1/99+1/100 >1/2
CM: 1/51 +1/52+1/53 +................+1/100 < 5/6
(1/51+1/52+1/53+....+1/100) : (1/1x2+1/3x4+...+1/99x100)
Có \(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}=+....+\frac{1}{99}-\frac{1}{100}\)
\(=\left(\frac{1}{1}+\frac{1}{3}+...+\frac{1}{99}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
=\(\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)-\left(1+\frac{1}{2}+...+\frac{1}{50}\right)\)
= \(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)
=> \(\left(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\right):\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\right)=1\)
Đúng 0
Bình luận (0)
(1/51+1/52+1/53+...+1/100)÷(1/1×2+1/3×4+1/4×5+...+1/99×100)
Tính A:
A=1/51 + 1/52 + 1/53 + ......... + 1/100