Cho hình thang ABCD,AB//CD.Trên cạnh AD,BC lần lượt là M,N sao cho MA/MD=NB/NC=K(0<K)
CM;MN//AB
Tính MN theo AB,CD và K
cho hình thang ABCD có AB//CD và AB<CD.Một đường thẳng a song song với các cạnh đấy AB,CD và cắt các cạnh bên AD,BC thứ tự tại M và N.Chứng minh rằng:
a)MA/AD=NB/BC
b)MA/MD=NB/NC
c)MD/AD=NC/BC
a: Gọi K là giao của AD và BC
Xét ΔKDC có AB//DC
nên KA/AD=KB/BC
=>KA/KB=AD/BC
Xét ΔKMN có AB//MN
nên KA/AM=KB/BN
=>KA/KB=AM/BN
=>AM/BN=AD/BC
=>AM/AD=BN/BC
b: AM/AD=BN/BC
=>AD/AM=BC/BN
=>AD/AM-1=BC/BN-1
=>\(\dfrac{AD-AM}{AM}=\dfrac{BC-BN}{BN}\)
=>DM/AM=NC/BN
=>MA/MD=BN/NC
c: AM/AD=BN/BC
=>AM/AD-1=BN/BC-1
=>(AM-AD)/AD=(BN-BC)/BC
=>-MD/AD=-CN/BC
=>MD/AD=CN/BC
Cho hình thang ABCD có AB//CD và AB <CD
đườg thăng song song với đáy AB cắt các cạnh bên AD,BC theo thứ tự tại M và N
Chứng minh rằng:
a)MA/AD=NB/BC
b)MA/MD=NB/NC
c)MD/DA=NC/CB
Cho hình thang ABCD (AB // CD) và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD , BC theo thứ tự tại M, N. Chứng minh rằng: a) MA NB AD BC = b) MA NB MD NC = c) MD NC DA CB = Hướng dẫn: Kéo dài các tia DA và CB cắt nhau tại E, áp dụng định lý Ta – lét trong tam giác và tính chất tỉ lệ thức để chứng minh
giúp mik với thanks nhiều nha:))
cho hình thang ABCD (AB//CD) đường thẳng ra // với hai đáy cắt các cạnh bên AB, CD lần lượt tại M,N sao cho MA/MD = 1/2. a) tính tỉ số NB/NC. b) cho AB=8,CD=17. tính MN
Cho hình thang ABCD có AB//CD, và AB<CD. Đường thẳng // với đáy AB cắt AD,BC tại M, N.
a. cm: MA / AD = NB /BC
b. MA / MD = NB/ NC
Cho hình thang ABCD có AB//CD và AB<CD. Đường thẳng // với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M,N.
CMR:
a)MA/AD=NB/BC
b)MA/MD=NB/NC
c)MD/DA=NC/CB
CHO HÌNH BÌNH HÀNH ABCD (AB//CD). LẤY ĐIỂM M TRÊN CẠNH AD, N TRÊN CẠNH BC SAO CHO \(\frac{MA}{MD}=\frac{NB}{NC}\)
CM MN//AB
Cho hình thang ABCD, AB=4cm, CD=7cm. Trên các cạnh AD và BC lần lượt lấy các điểm M và N sao cho MD=2MA, NC=2NB. Tính độ dài MN?
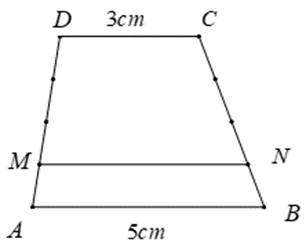
Cho hình thang ABCD có độ dài đáy AB=5cm; CD=3cm. Các điểm M, N lần lượt nằm trên các cạnh AD và BC sao cho MA= 1/4 AD, NB= 1/4BC. Nối M với N, ta được hai hình thang ABNM và CDMN. S của ABCD =16cm2. Tính độ dài MN.
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên
\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)
\(S_{ABCD}=S_{ACD}+S_{BCD}\)
\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)
\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)
Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD
\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)
C/m tương tự ta cũng có
\(S_{ABC}=S_{ABD}=10cm^2\)
Hai tg ABN và tg ABC có chung đường cao từ A->BC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)
đường cao từ N->AB là
\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)
Hai tg NCD và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)
\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)
Hai tg AMN và tg ADN có chung đường cao từ N->AD nên
\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)
\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)
Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN.
Bạn tự tính nốt nhé
Sabcd = 16cm² => (3+5)xHabcd =32 cm => Habcd = 4cm.
Điểm M và N lần lượt = 1/4 AD và BC nên chiều cao ABNM = 4:4 = 1cm. Chiều cao CD đến MN = 4-1= 3cm
Ta có: Sabnm + Smncd = 16cm² => (5+mn)+ (3+mn)x3 = 32cm
4mn+14=32cm => mn=4,5cm
Cho hình thang ABCD có độ dài hai đáy là AB = 5 cm ,CD = 3 cm .Các điểm M,N làn lượt nằm trên các cạnh AD,BC sao cho AD = 4 MA ,BC = 4 NB .Chia ABCD thành hai hình thang ABNM , CDMN .Biết diện tích hình thang ABCD = 16 cm ² a) Tính chiều cao của hình thang ABCD b) Tính độ dài đoạn MN
làm theo cách lớp 5