B1 Cho hình bình hành ABCD ( AB//CD) có AB = 2AD . Gọi I,K theo thứ tự là trung điểm của CD,AB
a) CMR : AI//CK
b) tính góc IAK nếu góc D = 120
cho hình bình hành abcd có ab = 2ad và A = 100độ .Gọi E, F theo thứ tự là trung điểm của các cạnh AB và CD . Tính Số Đo góc B
Cho hình bình hành ABCD có góc A = 120 độ và AB=2AD. Gọi E là trung điểm của AB
a,CMR DE vuông góc với EC
b,Xác định hình dạng của tứ giác AECD
a: Gọi F là trung điểm của DC
E là trung điểm của AB
=>\(AE=EB=\dfrac{AB}{2}\)
F là trung điểm của DC
=>\(FD=FC=\dfrac{DC}{2}\)
mà AB=DC
nên AE=EB=CF=FD=AB/2
mà \(AD=BC=\dfrac{AB}{2}\)
nên \(AE=EB=CF=FD=AD=BC\)
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
Hình bình hành AEFD có EA=AD
nên AEFD là hình thoi
=>EF=FD=DC/2
Xét ΔEDC có
EF là đường trung tuyến
\(EF=\dfrac{DC}{2}\)
Do đó: ΔEDC vuông tại E
=>DE\(\perp\)EC
b:
ABCD là hình bình hành
=>\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(\widehat{ABC}=180^0-120^0=60^0\)
Xét ΔBEC có BE=BC và \(\widehat{B}=60^0\)
nên ΔBEC đều
=>\(\widehat{BEC}=60^0\)
\(\widehat{BEC}+\widehat{AEC}=180^0\)(hai góc kề bù)
=>\(\widehat{AEC}+60^0=180^0\)
=>\(\widehat{AEC}=180^0-60^0=120^0\)
Xét tứ giác AECD có
AE//CD
nên AECD là hình thang
Hình thang AECD có \(\widehat{EAD}=\widehat{AEC}\)
nên AECD là hình thang cân
cho hình bình hành ABCD có AB = 2AD góc D = 70 độ . Vẽ BH vuông góc với AD ( H thuộc AD ) . Gọi M , N lần lượt lên trung điểm cạnh CD, AB
a, C/m tứ giác ANMD là hình thoi
b, Tính góc HMC
a: Xét tứ giác ANMD có
AN//MD
AN=MD
Do đó: ANMD là hình bình hành
mà AN=AD
nên ANMD là hình thoi
•Cho hình bình hành ABCD. Gọi I, K Theo Thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI , CK theo thứ tự ở M, N. Chứng minh rằng:
a) AI //CK
b) DM=MN=NB
c) Chứng minh CM đi qua trung điểm của AD, AN đi qua trung điểm của BC.
d) Chứng minh K, O, I thẳng hàng, với O là giao của 2 đường chéo AC và BD.
a: Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó:AKCI là hình bình hành
Suy ra: AI//CK
B1)Tứ giác ABCD có AD=BC, các tia DA và CB cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của AB, CD. Đường thẳng IK cắt các đường thẳng AD, BC theo thứ tự ở E,F. CMR; OEF là tam giác cân
B2) Hình thang ABCD (AB//CD) có AB=a, CD=b, BC= c, AD= d. Các tia phân giác của các góc A và D cắt nhau ở E. Các tia phân giác của các góc B và C cắt nhau ở F. Gọi M, N theo thứ tự là trung điểm của AD, BC.
a)CMR: 4 điểm M, E, F, N thẳng hàng
b) Tính các độ dài MN, MF, FN theo a,b,c,d
c) CMR: a+b= c+d thì E trùng với F
B3) Cho hình thang ABCD (AB//CD) có AB= AD+BC. CMR: các tia phân giác của góc C,D cắt nhau tại một điểm trên cạnh AB.
mk mới lên lớp 8 nên ko bít làm nhìn mún lòi mắt
Vậy Rộp Rộp Rộp, các bạn khác đang hỏi, bạn không trả lời mà đăng như thế lên làm gì ?
Cho hình bình hành ABCD, có AB = 2AD gọi E, F theo thứ tự là trung điểm của AB và CD.
a, CMR: AECF là hình bình hành
b, CMR: AEFD là hình thoi
c, AF cắt DE tại R, CE cắt BF tại S. CM: ERFS là hình chữ nhật
d, Gọi I và K lần lượt là giao điểm của BD với AF và BD với CE. CM: tam giác EIK cân.
Cho hình bình hành ABCD có AB = 2AD và góc D. = 70 độ . Gọi H là hình. chiếu của B trên AD, M là trung điểm của CD. Tính góc HMC
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông.
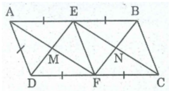
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.