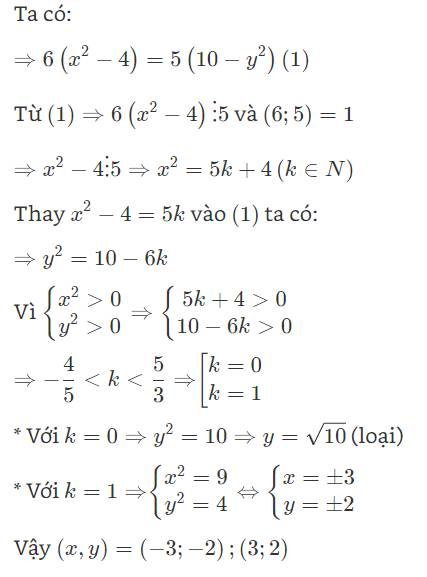_Tìm 2 cặp x,y nguyên dương thoả mãn: 4x3 + 17(2x-y)2 = 161312_ Mình tìm được (30;4) _giúp mình tìm cặp còn lại

Những câu hỏi liên quan
tìm các cặp (x;y) nguyên dương thoả mãn phương trình yx^3+17(2x-y)^2
Tìm tất cả các cặp số nguyên dương (x;y) thoả mãn
2x^2-xy-x-2y+1=0
tìm các cặp số nguyên dương (x,y) thoả mãn : \(6x^2+5y^2=74\)
Cuu Cần gấp !!!!![]()
số cặp số nguyên (x;y) thoả mãn (2x-5)(y-6)=17
_Tìm x , y , z nguyên dương thỏa mãn xy + xz + yz = 3xyz
_Cho x , y là các số dương và x + y = z . Tìm GTNN của N=(1-4:x^2)(1-4:y)
Tìm tất cả các cặp số nguyên dương (x;y) thoả mãn 4x2 = 3x + y2
Tìm cặp số nguyên (x;y) thoả mãn:
\(x^2y+xy-2x^2-3x+4=0\)
Với mỗi số nguyên dương n, gọi Sn là số cặp cặp số nguyên (x,y) thoả mãn x^2+y^2≤n^2
Xét điểm M(a;b) bất kì nằm trog ( tính cả biên ) của hình tròn ( \(C_n\)) : \(x^2+y^2\le n^2\)
Mỗi điểm M như vậy tương ứng với 1 và chỉ 1 hình vuông đơn vị S(M) mà M là đỉnh ở goc trái , phía dưới
Từ đó suy ra \(S_n\)= số hình vuông S (M) = tổng diện tích của S(M) với \(M\in\left(C_n\right)\)
Rõ ràng các hình vuông S(M) , với \(M\in\left(C_{ }_n\right)\)đều nằm trog hình tròn \(\left(C_{n+\sqrt{2}}\right):x^2+y^2\le\left(n+\sqrt{2}\right)^2\)
Do đó : \(S_n\le\pi\left(n+\sqrt{2}\right)^2\)(1)
Tương tự như vậy , ta thấy các hình vuông S(M) , với \(M\in\left(C_n\right)\)phủ kín hình tròn
\(\left(C_{n-\sqrt{2}}\right):x^2+y^2\le\left(n-\sqrt{2}\right)^2\)vì thế \(S_n\ge\pi\left(n-\sqrt{2}\right)^2\)(2)
Từ (1) và (2) suy ra \(\sqrt{\pi}\left(n-\sqrt{2}\right)\le\sqrt{S_n}\le\sqrt{\pi}\left(n+\sqrt{2}\right)\)
suy ra \(\sqrt{\pi}\left(1-\frac{\sqrt{2}}{n}\right)\le\frac{\sqrt{S_n}}{n}\le\sqrt{\pi}\left(1+\frac{\sqrt{2}}{n}\right)\)
Mà lim \(\sqrt{\pi}\left(1-\frac{\sqrt{2}}{n}\right)\)= lim\(\sqrt{\pi}\left(1+\frac{\sqrt{2}}{n}\right)=\sqrt{\pi}\)nên lim \(\sqrt{\frac{S_n}{n}}=\sqrt{\pi}\)
@ Huy @ Bài làm đánh đẹp lắm. Nhưng cô cũng không hiểu được rõ ràng là toán 6 sao có lim, phương trình đường tròn;... ( lớp 11 , 12 ) ở đây.
Lần sau chú ý giải Toán 6 không cần dùng kiến thức quá cao nhé.
Tuy nhiên đề bài bạn thiếu. Lần sau em có thể sửa lại đề bài trước rồi hẵng làm nha.
Tìm cặp số nguyên ( x , y ) thoả mãn
y2 = 3 - 2 . |2x + 3|