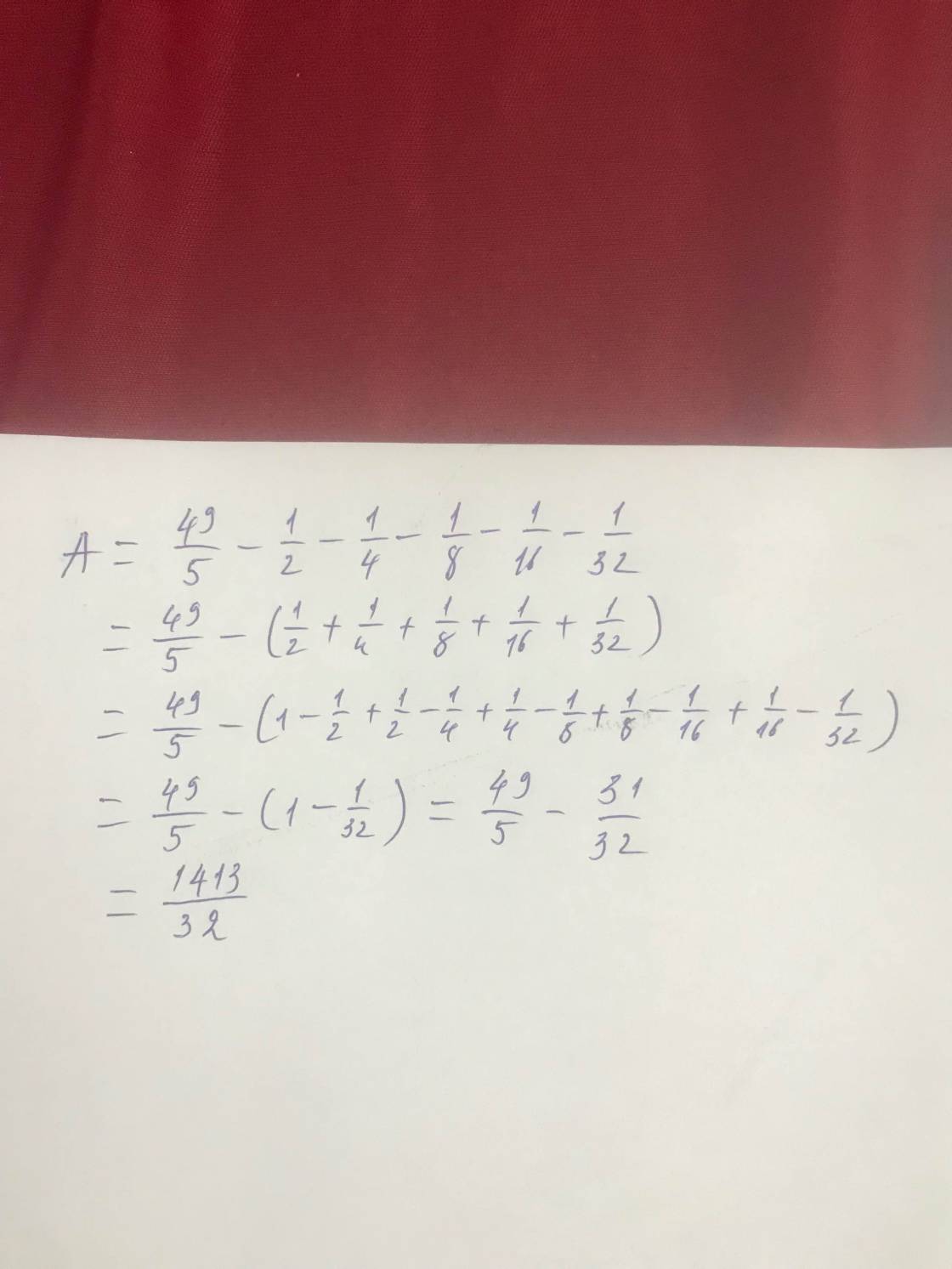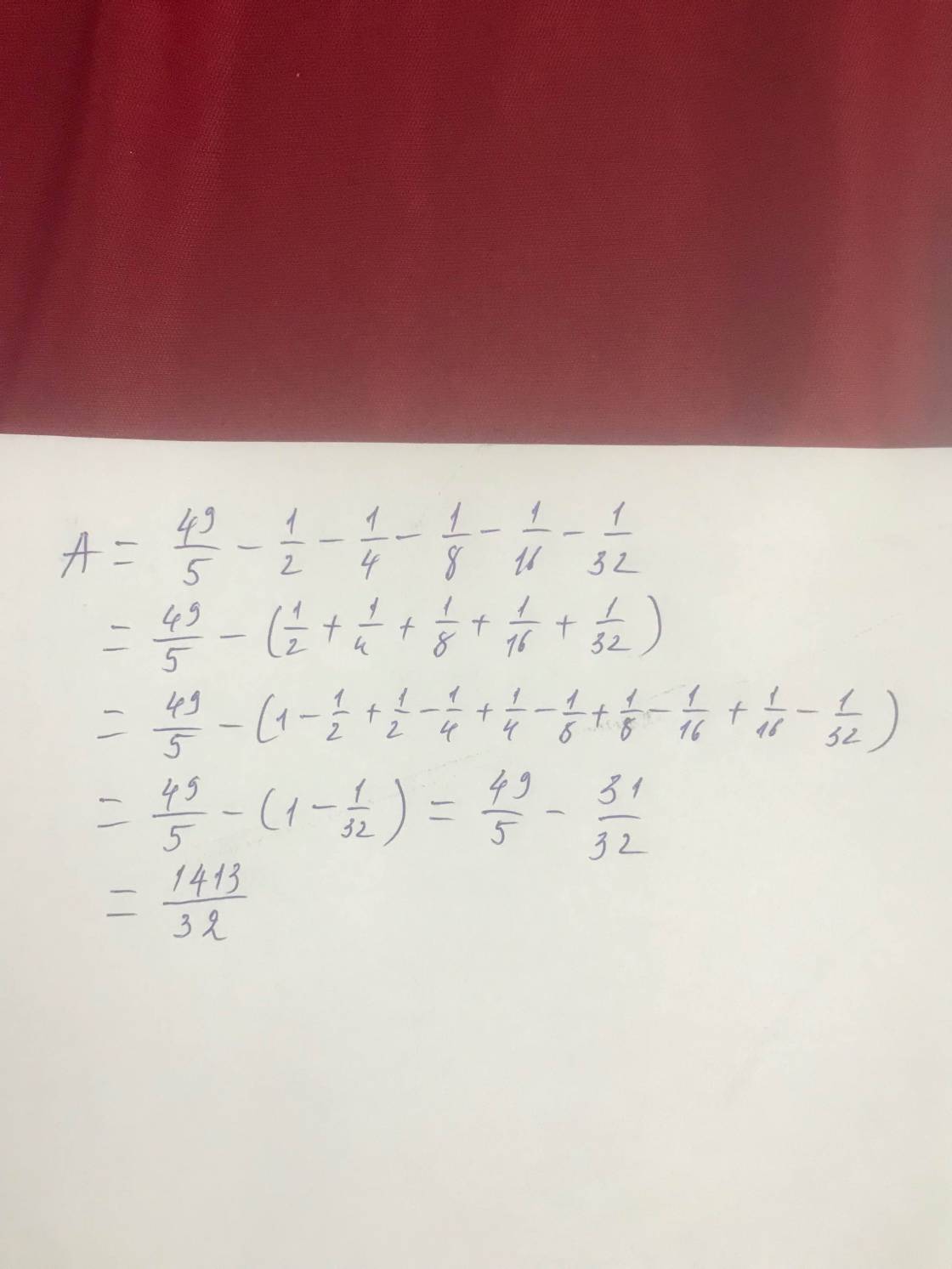tính bằng cách thuận tiện nhất B 1/2+1/4+1/8+1/16+1/32+1/64

Những câu hỏi liên quan
tính bằng cách thuận tiện nhất
A=1/2 + 1/4 + 1/8 + 1/16+ 1/32 + 1/64
đặt `A= 1/2 + 1/4 + 1/8 + 1/16+ 1/32 + 1/64`
`=> 2A = 2(1/2 + 1/4 + 1/8 + 1/16+ 1/32 + 1/64)`
`2A = 1+1/2 +1/4 +1/8+1/16 +1/32`
`=>A =2A -A =1+1/2 +1/4 +1/8+1/16 +1/32-1/2-1/4-1/8-1/16-1/32 -1/64`
`A = 1-1/64 = 64/64 -1/64 =63/64`
Đúng 3
Bình luận (0)
tính bằng cách thuận tiện nhất:
1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256
Đặt A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256
=> 2A = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
=> 2A - A = (1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128) - (1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256)
=> A = 1 - 1/256
=> A = 255/256
Vậy: ...
Đúng 0
Bình luận (0)
tính bằng cách thuận tiện nhất
1\2+1\4+1\8+1\16+1\32+1\64
voi lai phan so sau hon phan so truoc la 2 doi vi anh nhat linh a?
Đúng 0
Bình luận (0)
qua don giai lop bon da hoc roi goi y cho
buoc 1 : Dat A
buoc 2:nhan ca hai ve voi N
buoc 3: tru ca hai ve cho nhau
Đúng 0
Bình luận (0)
tính tổng các phân số sau bằng cách thuận tiện nhất:
1/2, 1/4, 1/8, 1/16, 1/32, 1/64
Tính bằng cách thuận tiện nhất chỉ cần đáp án thôi nhé.
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256
TL
= 255/256
Bn nhé
Tính bằng cách thuận tiện nhất: 49/5-1/2-1/4-1/8-1/16-1/32=
Tính bằng cách thuận tiện nhất :
49 /5 - 1/2 1/4 -1/8 -1/16 -1/32
\(A=\dfrac{49}{5}-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}\right)\)
\(A=\dfrac{49}{5}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{32}\right)\)
\(A=\dfrac{49}{5}-\left(1-\dfrac{1}{32}\right)=\text{}\dfrac{49}{5}-\dfrac{31}{32}\text{}\)
\(A=\dfrac{1413}{160}\text{}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính bằng cách thuận tiện:
a.A=1/2+1/4+1/8+1/16+1/32+1/64
b.B=1/3+1/9+1/27+1/81+1/243
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}\)
\(A=1-\frac{1}{64}\)
\(A=\frac{63}{64}\)
\(B=\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}\)
\(3B=1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}\)
\(3B-B=1-\frac{1}{243}\)
\(2B=\frac{242}{243}\)
\(B=\frac{242}{243}\div2\)
\(B=\frac{121}{243}\)
Đúng 0
Bình luận (0)
a.A=1/2+1/4+1/8+1/16+1/32+1/64
A= \(\frac{1}{1\cdot2}+\frac{1}{2\cdot2}+\frac{1}{2\cdot4}+\frac{1}{4\cdot4}+\frac{1}{4\cdot8}+\frac{1}{8\cdot8}\)
= \(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{8}\)
= 1 - 1/8 = 7/8
b.B=1/3+1/9+1/27+1/81+1/243
B= \(\frac{1}{1\cdot3}+\frac{1}{3\cdot3}+\frac{1}{3\cdot9}+\frac{1}{9\cdot9}+\frac{1}{9\cdot27}\)
= 1 - 1/27 = 26/27
Đúng 0
Bình luận (0)
tính bằng cách thuận tiện nhất
49/5 - 1/2 - 1/4 - 1/8 - 1/16 - 1/32