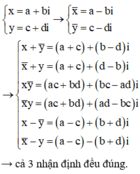Cho hai số x,y( y<x<0) thoã mãn x/y=3/5, x^2y^2=225

Những câu hỏi liên quan
a) cho x, y là hai số nguyên dương, biết | x | + | y | = 20 . Tính x + y
b) cho x, y là hai số nguyên âm , biết | x | + | y | = 20 . Tính x + y
Giúp với mai là nộp cho cô rồi: cho x,y là hai số nguyên dương biết |x| + |y| = 20 tính x + y típ nè cho x,y là hai số nguyên âm , biết |x|+|y| =20 tính x,y . Thank you very much !
Vi x,y la hai so nguyen duong=>|x|=x;|y|=y=>|x|+|y|=x+y=20 Vay x+y=20 NHO **** MINH NHA
Đúng 0
Bình luận (0)
Cho hai số x;y ( 0 > x > y ) .Biết x/2 = y/4 và x^4 . y^4 =16 . Tìm hai số x và y đó
Cho hai số x,y là hai số nguyên sao cho: /x/+/y/=2. Khi đó x,y lớn nhất có giá trị là ?
a, Cho x, y là hai số nguyên dương, biết | x | + | y | = 20.Tính x + y
b, Cho x, y là hai số nguyên âm, biết | x | + | y | = 20. Tính x + y
Giúp mik nha,mik đang cần gấp,ai nhanh mik tik
a. l x l + l y l = 20
= x + y =20
Vậy x + y =20
Đúng 0
Bình luận (0)
bạn nè, giá trị tuyệt đối của x thì bằng với x nếu x là số dương nhé.
Đúng 0
Bình luận (0)
a, vì /x/ +/y/ là 2 số nguyên dương
suy ra /x/=x;/y/=y
suy ra /x/+/y/=x+y=20
suy ra các số thỏa mãn điều kiện x+y=20 là
x=1 thì y=19 ngược lại
x=2 thì y=18 ngược lại
x=3 thì y=17 ngược lại
x=4 thì y=16 ngược lại
x=5 thì y=15 ngược lại
x=6 thì y=14 ngược lại
x=7 thì y =13 ngược lại
x=8 thì y=12 ngược lại
x=9 thì y =11 ngược lại
x=10 thì y=10
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hai số x,y biết 8^y=2^x+^8 và 3^x=9^y-^1
khi đó hai số x,y có tổng bằng
Cho hai số x, y là các số nguyên sao cho |x| + |y| = 2. Số cặp số x, y thỏa mãn là
Cho x,y là các số phức ta có các khẳng định sau: 1)
x
+
y
¯
v
à
x
¯
+
y
là hai số phức liên hợp của nhau. 2)
x
y
¯
v
à
x
¯
y
là hai số phức liên hợp của nhau. 3)
x
−
y...
Đọc tiếp
Cho x,y là các số phức ta có các khẳng định sau:
1) x + y ¯ v à x ¯ + y là hai số phức liên hợp của nhau.
2) x y ¯ v à x ¯ y là hai số phức liên hợp của nhau.
3) x − y ¯ v à x ¯ − y là hai số phức liên hợp của nhau.
Hỏi có bao nhiêu khẳng định đúng
A. không
B. một
C. hai
D. ba
Cho hai số thực x,y. Chứng minh rằng nếu xy+x+y=-1 thì trong hai số x,y có ít nhất một số bằng -1
Ta có : xy + x + y = -1
=> x(y + 1) + y + 1 = -1 + 1
=> (x + 1)(y + 1) = 0
=> \(\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\)(đpcm)
Vậy nếu xy + x + y = - 1 thì có ít nhất 1 số bằng - 1
xy + x + y = -1
<=> xy + x + y + 1 = 0
<=> x( y + 1 ) + 1( y + 1 ) = 0
<=> ( x + 1 )( y + 1 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\) ( đpcm )
\(xy+x+y=-1\)
\(< =>xy+x+y+1=0\)
\(< =>x\left(y+1\right)+\left(y+1\right)=0\)
\(< =>\left(x+1\right)\left(y+1\right)=0\)
\(< =>\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\)ez
Cho hai số x, y là các cặp số nguyên sao cho: |x| + |y| = 2. Số cặp (x, y) thỏa mãn là
Vì x,y nguyên mà |x| + |y| = 2
<= > x , y \(\le\) 2
TH1: |x| = 0 ; |y| = 2 => có 2 trường hợp
TH2: |x| = 1 ; |y| = 1 => có 4 trường hợp
TH3: |x| = 2 ; |y| = 0 => Có 2 trường hợp
Vậy có tất cả: 2 + 4 + 2= 8 trường hợp
Đúng 0
Bình luận (0)
TH1 : x = 1 và y = 2
TH2 : x = -1 và y = -1
TH3 : x = -2 hoặc 2 và y = 0
TH4 : x= 0 và y = -2 hoặc 2
**** đúng nha
Đúng 0
Bình luận (0)
|x|,|y| có thể lần lượt là 0;2, 1;1 hoặc 2;0
Vậy có 3 cặp (x,y) thỏa mãn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời