cần gấp ạ, trưa mình phải chụp gửi cô rồi,phiền các bạn ghi giả thuyết,kết luận với vẽ hình ạ:((

Những câu hỏi liên quan
cho hình bình hành ABCD các đường chéo cắt nhau ở O. Gọi E,F,G,H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, DOC, COD, DOA. Chứng minh rằng: EFGH là hình thoi
(yêu cầu vẽ hình, ghi giả thuyết và kết luận)
mình cần rất gấp mấy bạn thấy thì giải giúp mình nha
cho hình bình hành ABCD các đường chéo cắt nhau ở O. Gọi E,F,G,H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, DOC, COD, DOA. Chứng minh rằng: EFGH là hình thoi
(yêu cầu vẽ hình, ghi giả thuyết và kết luận)
mình cần rất gấp mấy bạn thấy thì giải giúp mình nha
cho hình bình hành ABCD các đường chéo cắt nhau ở O. Gọi E,F,G,H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, DOC, COD, DOA. Chứng minh rằng: EFGH là hình thoi
(yêu cầu vẽ hình, ghi giả thuyết và kết luận)
mình cần rất gấp mấy bạn thấy thì giải giúp mình nha
Các bạn giúp mik viết giả thiết kết luận cho hình trên với ạ mik đg cần gấp.cảm tạ ạ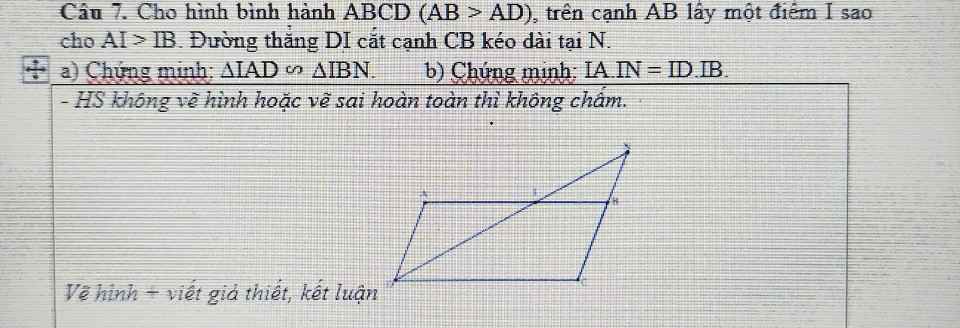
a: Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
b: ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
Đúng 0
Bình luận (0)
Các bạn giúp mik viết giả thiết kết luận cho hình trên với ạ mik đg cần gấp.cảm tạ ạ
Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
Đúng 0
Bình luận (0)
tứ giác ABCD có AB=BC và AC là tia phân giác của góc A . Chứng minh rằng ABCD là hình thang (viết giả thuyết và kết luận với vẽ hình)
giúp mik vs ạ mik đag cần gắp m.người ơi
m.người ơi
Xem chi tiết
giúp mik vs ạ mik đag cần gắp
BA=BC
=>góc BAC=góc BCA
=>góc BCA=góc DAC
=>AD//BC
=>ABCD là hình thang
Đúng 0
Bình luận (0)
Câu 3 câu H(x) thôi ạ còn câu 4,5 vẽ hình nêu giả thuyết kết luận
Bài 5:
a) Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABM=ΔEBM(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
Bài 5:
b) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc ở đáy)
\(\Leftrightarrow\widehat{MCB}+60^0=90^0\)
hay \(\widehat{MCB}=30^0\)(1)
Ta có: BM là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{MBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
Suy ra: MB=MC(Hai cạnh bên)
Xét ΔMBE vuông tại E và ΔMCE vuông tại E có
MB=MC(cmt)
ME chung
Do đó: ΔMBE=ΔMCE(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CE(Hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Vẽ hình minh họa, viết giả thiết- kết luận và chứng minh những định lý sau:
a,"hai góc đối đỉnh thì bằng nhau"
b,"hai đường thẳng phân biệt cùng vuông góc với một đường thảng thứ ba thì chúng song song với nhau"
giải giúp mình ạ mình cần gấp :<<
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
Đúng 0
Bình luận (0)
Mọi người giúp mình nhé! Trưa nay mình cần, các bạn giúp tớ vẽ hình với ạ
Ai giúp tớ đầu tiên tớ bình chọn nhé!