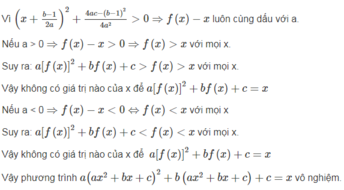cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Những câu hỏi liên quan
Đố. Đố em biết vì sao khi a 0 và phương trình
a
x
2
+
b
x
+
c
0
vô nghiệm thì
a
x
2
+
b
x
+
c
...
Đọc tiếp
Đố. Đố em biết vì sao khi a > 0 và phương trình a x 2 + b x + c = 0 vô nghiệm thì a x 2 + b x + c > 0 với mọi giá trị của x?
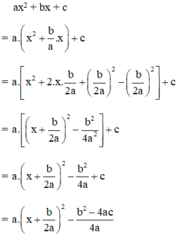
Ta có: a > 0 (gt),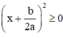 
với mọi x, a, b ⇒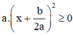 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
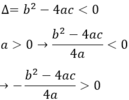
Vậy
a
x
2
+
b
x
+
c
= 
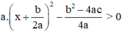với mọi x.
Đúng 0
Bình luận (0)
Đố. Đố em biết vì sao khi a > 0 và phương trình ax2 + bx + c = 0 vô nghiệm thì ax2 + bx + c > 0 với mọi giá trị của x?
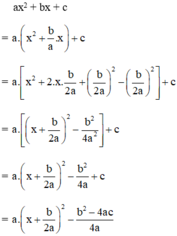
Ta có: a > 0 (gt),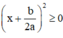 
với mọi x, a, b ⇒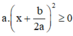 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
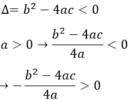
Vậy ax2 + bx + c =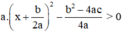 
với mọi x.
Đúng 0
Bình luận (0)
Chứng minh rằng nếu phương trình a
x
2
+ bx + c x (a
≠
0) vô nghiệm thì phương trình a
a
x
2
+
b
x
+
c
2
+ b(a...
Đọc tiếp
Chứng minh rằng nếu phương trình a x 2 + bx + c = x (a ≠ 0) vô nghiệm thì phương trình a a x 2 + b x + c 2 + b(a x 2 + bx + c) + c = x cũng vô nghiệm.
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
∆
b
2
–
4
a
c
. Phương trình đã cho vô nghiệm khi: A.
∆
0
B.
∆...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức ∆ = b 2 – 4 a c . Phương trình đã cho vô nghiệm khi:
A. ∆ < 0
B. ∆ = 0
C. ∆ ≥ 0
D. ∆ ≤ 0
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình có nghiệm
kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình có
hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
Δ
b
2
-
4
a
c
.
Phương trình đã cho vô nghiệm khi: A.
△
0 B.
△
0 C.
△
≥
0 D.
△
...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức Δ = b 2 - 4 a c . Phương trình đã cho vô nghiệm khi:
A. △ < 0
B. △ = 0
C. △ ≥ 0
D. △ ≤ 0
Đáp án A
Xét phương trình bậc hai một ẩn a x 2 + b x + c = 0 ( a ≠ 0 ) và biệt thức Δ = b 2 - 4 a c
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép
x
1
=
x
2
= 
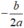
• TH3: Nếu thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 
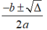
Đúng 0
Bình luận (0)
Viết chương trình: Tìm nghiệm x của phương trình ax2 + bx + c = 0 với a, b, c nhập từ bàn phím (các trường hợp 2 nghiệm, nghiệm kép, vô nghiệm)
--------------------------
Mọi người giúp em với ạ, em cảm ơn
import math
a = float(input("Nhập a: "))
b = float(input("Nhập b: "))
c = float(input("Nhập c: "))
d = b**2 - 4*a*c
if d > 0:
x1 = (-b + math.sqrt(d)) / (2*a)
x2 = (-b - math.sqrt(d)) / (2*a)
print("Phương trình có hai nghiệm: x1 =", x1, "và x2 =", x2)
elif d == 0:
x = -b / (2*a)
print("Phương trình có nghiệm kép: x =", x)
else:
print("Phương trình không có nghiệm thực."
Đúng 2
Bình luận (1)
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
Nêu điều kiện để phương trình
a
x
2
+
b
x
+
c
0
(a ≠...
Đọc tiếp
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc haiax2 + bx + c 0 (a ≠ 0)Nêu điều kiện để phương trình ax2 + bx + c 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình1954x2 + 21x – 1975 0Nêu điều kiện để phương trình ax2 + bx + c 0 (a ≠ 0) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình2005x2 + 104x – 1901 0
Đọc tiếp
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
ax2 + bx + c = 0 (a ≠ 0)
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954x2 + 21x – 1975 = 0
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005x2 + 104x – 1901 = 0
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
b
2
b
’
;
Δ
b
2
−
a
c
Phương trình đã cho vô nghiệm khi? A.
Δ...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2 b ’ ; Δ ' = b ' 2 − a c Phương trình đã cho vô nghiệm khi?
A. Δ ' > 0
B. Δ ' = 0
C. Δ ' ≥ 0
D. Δ ' < 0
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu Δ ' < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu Δ ' = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu Δ ' > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)