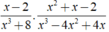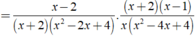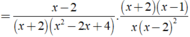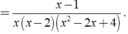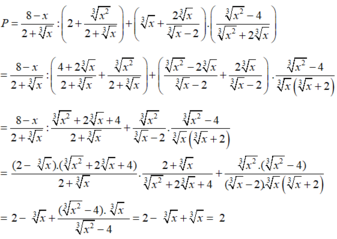x:8=2x3

Những câu hỏi liên quan
Thực hiện các phép tính sau:
x
-
2
x
3
+
8
.
x
2
+
x
-
2
x
3
-
4
x
2
+
4...
Đọc tiếp
Thực hiện các phép tính sau: x - 2 x 3 + 8 . x 2 + x - 2 x 3 - 4 x 2 + 4 x
Tìm hệ số của mỗi đa thức sau
a) f (x) = 3x2 + 5x3 - 7x - 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
Đúng 5
Bình luận (0)
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
Đúng 2
Bình luận (4)
1/ Thực hiện các phép tính sau: a) (2x - y)(4x2 - 2xy + y2) b) (6x5y2 - 9x4y3 + 15x3y4): 3x3y2 c) (2x3 - 21x2 + 67x - 60): (x - 5) d) (x4 + 2x3 +x - 25):(x2 +5) e) (27x3 - 8): (6x + 9x2 + 4)
a) \(\left(2x-y\right)\left(4x^2-2xy+y^2\right)\)
\(=8x^3-4x^2y+2xy^2-4xy^2+2xy^2-y^3\)
\(=8x^3-8x^2y+4xy^2-y^3\)
b) \(\left(6x^5y^2-9x^4y^3+15x^3y^4\right):3x^3y^2\)
\(=2x^2-3xy+5y^2\)
Đúng 1
Bình luận (0)
Hệ phương trình
x
+
y
+
2
x
y
2
x
3
+
y
3...
Đọc tiếp
Hệ phương trình x + y + 2 x y = 2 x 3 + y 3 = 8 có bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 4
Đặt X = x + y P = x . y điều kiện S 2 ≥ 4 P hệ phương trình đã cho trở thành
S + 2 P = 2 S S 2 − 3 P = 8 ⇔ P = 2 − S 2 S S 2 − 6 − 3 S 2 = 8
⇒ 2 S 3 + 3 S 2 – 6 S - 16 = 0 ⇔ ( S – 2 ) ( 2 S 2 + 7 S + 8 ) = 0 ⇔ S = 2 ⇒ P = 0
Hay x + y = 2 x . y = 0 ⇔ x = 0 ; y = 2 x = 2 ; y = 0
Vậy hệ có hai nghiệm
Đáp án:C
Đúng 0
Bình luận (0)
Phân tích
a,(x2 + x + 2)3 - (x+1)3 x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A x4 + 2x3 + 3x2 + 2x+4 d,B x4 + 4x3 + +8x2 + 8x + 4
e, C x4 - 2x3 + 5x2 - 4x + 4
Đọc tiếp
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
b: \(\left(x^2+10x+8\right)^2-\left(8x+4\right)\left(x^2+8x+7\right)\)
\(=\left\lbrack\left(x^2+8x+7\right)+\left(2x+1\right)\right\rbrack^2-4\left(2x+1\right)\left(x^2+8x+7\right)\)
\(=\left(x^2+8x+7\right)^2+2\left(x^2+8x+7\right)\left(2x+1\right)+\left(2x+1\right)^2-4\left(2x+1\right)\left(x^2+8x+7\right)\)
\(=\left(x^2+8x+7\right)^2-2\left(x^2+8x+7\right)\left(2x+1\right)+\left(2x+1\right)^2\)
\(=\left(x^2+8x+7-2x-1\right)^2=\left(x^2+6x+6\right)^2\)
d: \(B=x^4+4x^3+8x^2+8x+4\)
\(=x^4+2x^3+2x^2+2x^3+4x^2+4x+2x^2+4x+4\)
\(=x^2\left(x^2+2x+2\right)+2x\left(x^2+2x+2\right)+2\left(x^2+2x+2\right)\)
\(=\left(x^2+2x+2\right)\left(x^2+2x+2\right)=\left(x^2+2x+2\right)^2\)
e: \(C=x^4-2x^3+5x^2-4x+4\)
\(=x^4-x^3+2x^2-x^3+x^2-2x+2x^2-2x+4\)
\(=x^2\left(x^2-x+2\right)-x\left(x^2-x+2\right)+2\left(x^2-x+2\right)=\left(x^2-x+2\right)\left(x^2-x+2\right)\)
\(=\left(x^2-x+2\right)^2\)
Đúng 0
Bình luận (0)
y x 1/2x3/4+y:8/5-y/2=1/2
\(yX\frac{1}{2}X\frac{3}{4}+y:\frac{8}{5}-\frac{y}{2}=\frac{1}{2}\)
\(yX\frac{3}{8}+yX\frac{5}{8}-y:2=\frac{1}{2}\)
\(yX\left(\frac{3}{8}+\frac{5}{8}\right)-y:\frac{2}{1}=\frac{1}{2}\)
\(yX1-yX\frac{1}{2}=\frac{1}{2}\)
\(yX\left(1-\frac{1}{2}\right)=\frac{1}{2}\)
\(yX\frac{1}{2}=\frac{1}{2}\)
\(y=\frac{1}{2}:\frac{1}{2}\)
\(y=1\)
Đúng 0
Bình luận (0)
Cho biểu thức sau ,với x 0 và x ≠ 8. Rút gọn P ta được ?
P
8
−
x
2
+
x
3
:
2
+
x
2
3
2
+
x
3...
Đọc tiếp
Cho biểu thức sau ,với x > 0 và x ≠ 8. Rút gọn P ta được ?
P = 8 − x 2 + x 3 : 2 + x 2 3 2 + x 3 + x 3 + 2 x 3 x 3 − 2 . x 2 3 − 4 x 2 3 + 2 x 3
A. 2
B. 2 - 2 x 3
C. x 3
D. 1/2
thực hiện phép chia
(-3x3 + 5x2 - 9x + 15) : (-3 + 5)
(x4 - 2x3 + 2x -1) : (x2 - 1)
(5x4 + 9x3 - 2x2 - 4x -8) : (x-1)
(5x3 + 14x2 + 12x + 8) : (x+2)
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
d) Ta có: \(\dfrac{5x^3+14x^2+12x+8}{x+2}\)
\(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}\)
\(=\dfrac{5x^2\left(x+2\right)+4x\left(x+2\right)+4\left(x+2\right)}{x+2}\)
\(=5x^2+4x+4\)
Đúng 1
Bình luận (0)
thực hiện phép chia
(-3x3 + 5x2 - 9x + 15) : (-3 + 5)
(x4 - 2x3 + 2x -1) : (x2 - 1)
(5x4 + 9x3 - 2x2 - 4x -8) : (x-1)
(5x3 + 14x2 + 12x + 8) : (x+2)
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
Đúng 0
Bình luận (0)