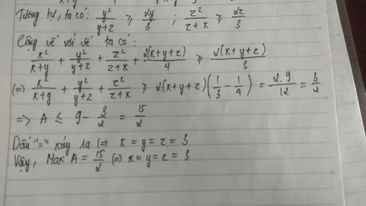Tìm x, y thuộc z thỏa mãn x+xy+y = 9

Những câu hỏi liên quan
tìm x; y thuộc Z thỏa mãn: x+xy+y = 9
tìm x,y thuộc Z thỏa mãn x+xy+y=9
x+xy+y=9
=> x(y+1)+y+1=10
=> x(y+1)+(y+1)=10
=> (x+1)(y+1)=10
sau đó làm giống bạn Nobita Kun
ủng hộ mik nha
Đúng 0
Bình luận (0)
x + xy + y = 9
=> x(y + 1) + (y + 1) = 10
=> (x + 1)(y + 1) = 10
=> 10 chia hết cho x + 1
Ta có bảng:
| x+1 | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| x | 0 | -2 | 1 | -3 | 4 | -6 | 9 | -11 |
| y+1 | 10 | -10 | 5 | -5 | 2 | -2 | 1 | -1 |
| y | 9 | -11 | 4 | -6 | 1 | -3 | 0 | -2 |
Vậy....
Đúng 0
Bình luận (0)
Tìm x,y thuộc Z thỏa mãn: x+xy+y=9
x+xy+y=9
=>x+xy+y+1=10
=>(x+xy)+(y+1)=10
=>x.(y+1)+(y+1)=10
=>(y+1)(x+1)=10=1.10=10.1=(-1).(-10)=(-10).(-1)=2.5=5.2=(-2).(-5)=(-5).(-2)
Ta có bảng sau:
| (x+1) ; (y+1) | 1;10 | 10;1 | -1;-10 | -10;-1 | 2;5 | 5;2 | -2;-5 | -5;-2 |
| (x;y) | (0;9) | (9;0) | (-2;-11) | (-11;-2) | (1;4) | (4;1) | (-3;-6) | (-6;3) |
Vậy các cặp x,y tìm dc là:
| (0;9) | (9;0) | (-2;-11) | (-11;-2) | (1;4) | (4;1) | (-3;-6) | (-6;3) |
Lưu ý: (a;b) thì x=a;y=b nha bạn
Đúng 1
Bình luận (0)
1.Tìm x;y thuộc N : x^3 -7=y^2
2.Tìm p;q thuộc P và x thuộc z thỏa mãn: x^5+px+3q=0
3, Tìm x;y thuộc Z thỏa mãn 6x^3-xy(11x+3y)+2y^3=6
cho x,y,z >0 thỏa mãn x+y+z=9 Tìm max A=xy/x+y + yz/y+z + zx/z+x
Ta có:\(A=\dfrac{xy}{x+y}+\dfrac{yz}{y+z}+\dfrac{zx}{z+x}\)
\(=\dfrac{x\left(x+y\right)-x^2}{x+y}+\dfrac{y\left(y+z\right)-y^2}{y+z}+\dfrac{z\left(z+x\right)-z^2}{z+x}\)
\(=\left(x+y+z\right)-\left(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\right)\)
Ta có:\(\dfrac{x^2}{x+y}+\dfrac{x+y}{9}\ge2\sqrt{\dfrac{x^2}{x+y}.\dfrac{x+y}{9}}=\dfrac{2x}{3}\)
Tương tự,ta có:\(\dfrac{y^2}{y+z}+\dfrac{y+z}{9}\ge\dfrac{2y}{3};\dfrac{z^2}{z+x}+\dfrac{z+x}{9}\ge\dfrac{2z}{3}\)
Cộng vế với vế ta có:
\(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}+\dfrac{2\left(x+y+z\right)}{4}\ge\dfrac{2\left(x+y+z\right)}{3}\)
\(\Leftrightarrow\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\ge\dfrac{2\left(x+y+z\right)}{3}-\dfrac{2\left(x+y+z\right)}{4}=\dfrac{2.9}{3}-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow A\le9-\dfrac{3}{2}=\dfrac{15}{2}\)
Dấu "=" xảy ra ⇔ x=y=z=3
Vậy,Max A=\(\dfrac{15}{2}\) ⇔ x=y=z=3
Đúng 0
Bình luận (0)
1.cho x,y,z thuộc R thỏa mãn x+y+z+xy+xz+yz=6. Tìm GTNN của : x^2+y^2+z^2
2. cho x,y>0 thỏa mãn x+1/y<=1. tìm GTNN: A=x/y+y/x
Tìm x,y Thuộc Z thỏa mãn x\(^2\)-xy+x-3y = 1
tìm các cặp x,y thuộc z thỏa mãn
xy+x-y=0
X THOẢN MÃN VỚI DIEUEDF KIỆN X=0 VÀ Y=0
Đúng 0
Bình luận (0)
Tìm x, y thuộc z thỏa mãn:
3(x^2+xy+y^2) = x+8y