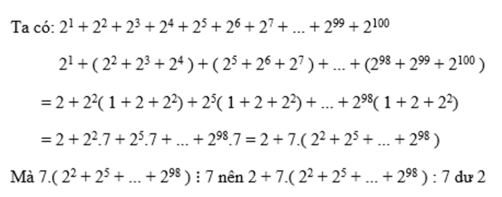A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016

=7(1+2^3+...+2^2013)+2^2016

Vì 2^2016 chia 7 dư 1

nên A chia 7 dư 1

Nếu bớt số càn tìm đi đúng bằng số dư khi chia số đó cho 23 thì được số mới chia hết cho 23

Sô mới là

23x21=483

Khi chia số mới cho 92 ta được thương là 5 và dư 23

Hiệu số dư của hai phép chia khi chia số cần tìm và số mới cho 92 là

30‐23=7

Số cần tìm là

483+7=490 

Nếu bớt số càn tìm đi đúng bằng số dư khi chia số đó cho 23 thì được số mới chia hết cho 23

Sô mới là

23x21=483

Khi chia số mới cho 92 ta được thương là 5 và dư 23

Hiệu số dư của hai phép chia khi chia số cần tìm và số mới cho 92 là

30‐23=7

Số cần tìm là

483+7=490 

So A la 490 .

k minh nha!

Gọi thương của phép chia a:21 là x, a:27 là y  (x,y thuộc N*)

Ta có: 21.x+3=27.y+12

<=> 21x=27y+9

<=> 7x=9y+3=3(3y+1)

=> \(x=\frac{3\left(3y+1\right)}{7}\)

Mà x thuộc N* => 3y+1 phải chia hết cho 7 => 3y+1=(1,7)

+/ 3y+1=1 => y=0 (Loại)

+/ 3y+1=7 => y=2 (Nhận)

=> x=3

Số cần tìm là: a=3.21+3=66

Đáp số: a=66

Ta có

  2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100

= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )

= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2

= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98

Mà  7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7  

Nên  2 + 7 2 2 + 2 5 + . . . + 2 98 : 7   d ư   2

\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)

\(2S=2^2+2.2^3+3.2^4+...+2016.2^{2017}\)

\(2S-S=S=\text{​​}\text{​​}\text{​​}\text{​​}2^2+2.2^3+3.2^4+...+2016.2^{2017}-2-2.2^2-3.2^3-...-2016.2^{2016}\)

\(S=2\left(0-1\right)+2^2\left(1-2\right)+2^3\left(2-3\right)+...+2^{2016}\left(2015-2016\right)+2^{2017}.2016\)

\(S=-\left(2+2^2+2^3+...+2^{2016}\right)+2^{2017}.2016\)

\(\)Đặt \(A=2+2^2+2^3+...+2^{2016}\)

\(2A=2^2+2^3+2^4+...+2^{2017}\)

\(2A-A=A=2^2+2^3+2^4+...+2^{2017}-2-2^2-2^3-...-2^{2016}\)

\(A=2^{2017}-2\)

Thay vào S ta được:
\(S=-2^{2017}+2+2^{2017}.2016\)

\(S=2^{2017}.2015+2\)

Ta có \(S+2013=2^{2017}.2015+2+2013\)

\(S+2013=2^{2017}.2015+2015\)

\(S+2013=2015\left(2^{2017}+1\right)\)

Suy ra \(S+2013⋮2^{2017}+1\)

Vậy \(S+2013⋮2^{2017}+1\) (đpcm)

cái này dễ lắm lun

\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)

\(S=2+2^3+3.2^3+...+2016.2^{2016}\)

\(S=2+2^3\left(1+3+...+2016.2^{2013}\right)\)

\(S=2+8.\left(1+3+...+2016.2^{2013}\right)\)

Suy ra \(S\) chia \(8\) dư \(2\)

Vậy \(S\) chia \(8\) dư \(2\)

Gửi bạn nha, bài này làm hơi dài ^^

Ta có A=2⁰+2¹+2²+2³+...2¹⁰⁰

2A=2¹+2²+...+2¹⁰¹

2A-A=(2¹+2²+...+2¹⁰⁰)-(2⁰+2¹+...+2¹⁰⁰)

A=2¹⁰¹-1

Mà 2¹⁰¹-1=(........02)-1=........01 chia 100 dư 1

Chúc bạn học tốt.