55*32/33*56
Những câu hỏi liên quan
tinh nhanh :55*32/33*56
20042004*2006/20062006*2000
55x32/33x56
=11x8x5x4/11x8x3x7
=5x4/3x7
=20/21
20042004x2006/20062006x2000
=10001x2004x2006/10001x2006x2000
=2004/2000=501/500
Đúng 0
Bình luận (0)
Tính nhanh :
55 x 32 = ?
33 x 56 = ?
(55x32)/ (33x56)
= (5x4) / (3x7)
=20/21
Trả lời: 20/21
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tính nhanh;
a,55*32/33*56
b,20042004*2006/20062006*2000
Tính nhanh:(chỉ có 5 phút để trả lời)
42 + 43 + 44 + 45 - 32 - 33 - 34 - 35
(64+ 65+ 66+ 67+ 68) - (54 + 55 + 56 + 57 + 58)
42 + 43 + 44 + 45 - 32 - 33 - 34 - 35
= (42 - 32)+(43 - 33)+(44 - 34)+(45 - 35)
= 10+10+10+10
= 40
(64+65+66+67+68) - (54+55+56+57+58)
= 64+65+66+67+68 - 54-55-56-57-58
= (64 - 54)+(65 - 55) +(66 - 56) + (67- 57) + (68 -58)
= 10+10+10+10+10
= 50
Đúng 0
Bình luận (0)
câu 1 40
câu 2 50
nha
Bài 1: Tính: A31+33+35+37+...+3111 B32+34+36+...+3200 C51+53+55+...+599 D 52+54+56+...+5100Bài 2: Chứng minh các phân số sau tối giản với n ϵ Na) dfrac{2n+1}{n+1} b)dfrac{2n+3}{3n+4}
Đọc tiếp
Bài 1: Tính: A=31+33+35+37+...+3111
B=32+34+36+...+3200
C=51+53+55+...+599
D= 52+54+56+...+5100
Bài 2: Chứng minh các phân số sau tối giản với n ϵ N
a) \(\dfrac{2n+1}{n+1}\) b)\(\dfrac{2n+3}{3n+4}\)
Bài 1:
1) \(9A=3^3+3^5+...+3^{113}\)
\(\Rightarrow8A=9A-A=3^3+3^5+...+3^{113}-3-3^3-...-3^{111}=3^{113}-3\)
\(\Rightarrow A=\dfrac{3^{113}-3}{8}\)
2) \(9B=3^4+3^6+...+3^{202}\)
\(\Rightarrow8B=9B-B=3^4+3^6+...+3^{202}-3^2-3^4-...-3^{200}=3^{202}-3^2=3^{202}-9\)
\(\Rightarrow B=\dfrac{3^{202}-9}{8}\)
3) \(25C=5^3+5^5+...+5^{101}\)
\(\Rightarrow24C=25C-C=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}=5^{101}-5\)
\(\Rightarrow C=\dfrac{5^{101}-5}{24}\)
4) \(25D=5^4+5^6+...+5^{102}\)
\(\Rightarrow24D=25D-D=5^4+5^6+...+5^{102}-5^2-5^4-...-5^{100}=5^{102}-25\)
\(\Rightarrow D=\dfrac{5^{102}-25}{24}\)
Đúng 1
Bình luận (0)
Bài 2:
a) Gọi d là UCLN(2n+1,n+1)
\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\n+1⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\2n+2⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮d\Rightarrow1⋮d\)
Vậy 2n+1 và n+1 là 2 số nguyên tố cùng nhau
\(\Rightarrow\dfrac{2n+1}{n+1}\) là phân số tối giản
b) Gọi d là UCLN(2n+3,3n+4)
\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}6n+9⋮d\\6n+8⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+9\right)-\left(6n+8\right)⋮d\Rightarrow1⋮d\)
\(\Rightarrow\dfrac{2n+3}{3n+4}\) là phân số tối giản
Đúng 1
Bình luận (2)
56:53+32:33-34.3
`5^6 : 5^3 +3^2 : 3^3 - 3^4 . 3`
`= 5^(6-3)+ (3^2)/(3^3) - 3^(4+1)`
`= 5^3 + 9/27 - 3^5`
`= 125 + 1/3 -243`
`=-353/3`
Đúng 0
Bình luận (0)
Điền vào ô vuông các dấu thích hợp (; ; ):a)
2
3
.
5
+
3
4
.
2
-
4
.
(
5
7
:
5
5
)
□
15
:
(
3
5
:
3
4
)
+
5
.
2
4
-
7
2
-
4
;
b)...
Đọc tiếp
Điền vào ô vuông các dấu thích hợp (=; <; >):
a) 2 3 . 5 + 3 4 . 2 - 4 . ( 5 7 : 5 5 ) □ 15 : ( 3 5 : 3 4 ) + 5 . 2 4 - 7 2 - 4 ;
b) ( 3 5 . 3 7 ) : 3 1 0 + 5 . 2 4 □ 5 . 2 2 . 2 3 - 4 . ( 5 8 : 5 6 ) ;
c) 2 [ ( 7 - 3 3 : 3 2 ) : 2 2 + 99 ] - 100 □ 3 4 . 2 + 2 3 . 5 - 7 ( 5 2 - 5 ) ;
d) 207 : { 2 ^ 3 . [ ( 156 - 128 ) : 14 ] + 7 ] □ 117 : { [ 79 - 3 ( 3 ^ 3 - 17 ) ] : 7 + 2 }
Đặt tính rồi tính:
63 + 25 87 - 14 31 + 56
94 - 34 62 - 62 55 - 33
- Đặt tính : Viết các chữ số cùng hàng thẳng cột với nhau.
- Tính : Cộng, trừ lần lượt từ hàng đơn vị đến hàng chục.
Đúng 0
Bình luận (0)
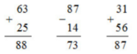
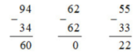
63 + 25 = 88 87 - 14 = 73 31 + 56 = 87
94 - 34 = 60 62 - 62 = 0 55 - 33 = 22
32.66-32+33+55
32 . 66 - 32 + 33 + 55
=2112 - 32 + 33 + 55
= 2080 + 33 + 55
= 2113 + 55
= 2168
Đúng 0
Bình luận (0)
32.66-32+33+55
=2112-32+33+55
=2080+33+55
=2113+55
=2168
Đúng 0
Bình luận (0)
32 . 66 - 32 + 33 + 55
=2112 - 32 + 33 + 55
= 2080 + 33 + 55
= 2113 + 55
= 2168
Đúng 0
Bình luận (0)