
Những câu hỏi liên quan
Giải phương trình với nghiệm tự nhiên: \(3^x+1=2^y\)
help me
1, giải phương tình nghiệm nguyên dương x^2y+x+y=xy^2z+yz+7z
2,giải phương trình nghiệm tự nhiên 2^x+3^y=z^2
3,giải phương trình nghiệm nguyên dương x^2+x+1=xyz-z
giải phương trình với nghiệm tự nhiên : 31(xyzt+xy+xt+zt+1)=40(yzt+y+t)
Cho hệ phương trình:
\(\hept{\begin{cases}2x-3y=m\\3x+4y=m+2\end{cases}} \)
a) Giải phương trình với m=1
b) Tìm giá trị nguyên của m để hệ phương trình có nghiệm là những cặp số tự nhiên
Giải phương trình nghiệm tự nhiên \(3\left(x^2+x\right)+7=y^3\)
Cho hệ phương trình \(\hept{\begin{cases}2x-3y=m\\3x+4y=m+2\end{cases}}\)
a, Giải hệ phương trình với m=1
b, Tìm giá trị nguyên của m để hệ phương có nghiệm là những cặp số tự nhiên
Có bao nhiêu số tự nhiên m để phương trình sau có nghiệm
e
m
+
e
3
m
2
x
+
1
-
x
2
1
+...
Đọc tiếp
Có bao nhiêu số tự nhiên m để phương trình sau có nghiệm e m + e 3 m = 2 x + 1 - x 2 1 + x 1 - x 2
A.2
B.0
C.Vô số
D.1
Có bao nhiêu số tự nhiên m để phương trình sau có nghiệm ?
e
m
+
e
3
m
2
x
+
1
-
x
2
1
+
x
1
-...
Đọc tiếp
Có bao nhiêu số tự nhiên m để phương trình sau có nghiệm ?
e m + e 3 m = 2 x + 1 - x 2 1 + x 1 - x 2 .
A. 2
B. 0
C. vô số
D. 1
ĐKXD:
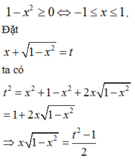
Ta có:
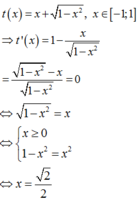
BBT:
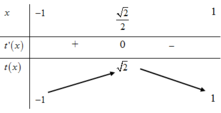
Từ BBT ta có: t ∈ - 1 ; 2 .
Khi đó phưng trình trở thành:
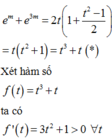
Hàm số đồng biến trên R Hàm số đồng biến trên - 1 ; 2 .
Từ
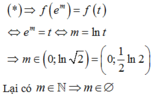
Chọn B.
Đúng 0
Bình luận (0)
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+30 và ( a+1)x-a+202/ Bất phương trình: 5x/5 - 13/21 + x/15 9/25- 2x/35 có nghiệm là....3/ Bất phương trình: 5x-1 2x/5 + 3 có nghiệm là...4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) (4x/3x-x^2) có nghiệm nguyên lớn nhất là...5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 2x -166/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 12 - 2x/37/ Bất phương trình: 2(x-1) - x 3(x-1) - 2x-5 có t...
Đọc tiếp
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Xem thêm câu trả lời
Giải phương trình với nghiệm tự nhiên:
a, \(2^x+2^y=2^z\)
b, \(2^x+2^y+2^z=552\)(với x<y<z)
b/ \(2^x+2^y+2^z=552\)
\(\Leftrightarrow2^x\left(1+2^{y-x}+2^{z-x}\right)=2^3.69\)
\(\Leftrightarrow\hept{\begin{cases}x=3\\1+2^{y-x}+2^{z-x}=69\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=3\\2^y+2^z=544\left(1\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow2^y\left(1+2^{z-y}\right)=2^5.17\)
\(\Leftrightarrow\hept{\begin{cases}y=5\\1+2^{z-y}=17\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=5\\z=9\end{cases}}\)
Vậy \(x=3;y=5;z=9\)
a/ Dễ thấy: \(z>x,y\)
Xét \(x>y\)
\(\Rightarrow2^x\left(1+2^{y-x}-2^{z-x}\right)=0\)
Loại vì \(2^x\left(1+2^{y-x}-2^{z-x}\right)< 0\)
Tương tự cho trường hợp \(x< y\)
Xét \(x=y\)
\(2^x+2^y=2^z\)
\(\Leftrightarrow2^{x+1}=2^z\)
\(\Leftrightarrow x+1=z\)
Vậy nghiệm là: \(x=y=z-1\)


















