giải giúp kik với ak, nhanh nah mình rất gấp nhaaaa

Những câu hỏi liên quan
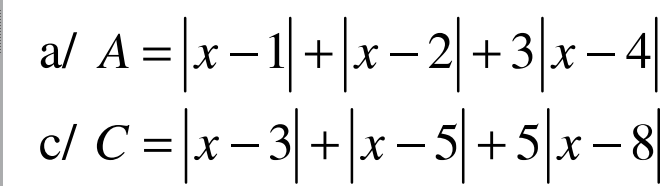
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
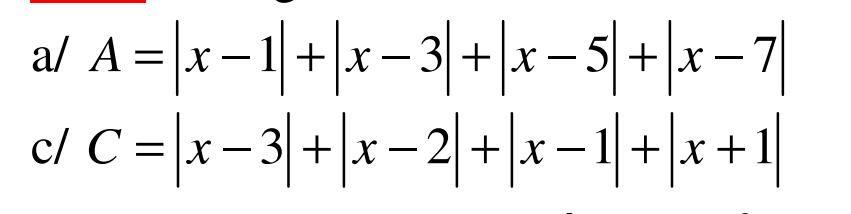
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
https://hoc24.vn/cau-hoi/minh-can-rat-rat-gap-loi-giai-chi-tiet-2-phan-nay-de-bai-la-tinh-gtnn-moi-ng-giup-minh-voiiiiiiiiiiiiiiiiiiiii-ak-minh-cam-on.1527826665808
Mình làm ở đây rồi bạn nhé. Bạn vào link này tham khảo.
Đúng 0
Bình luận (0)
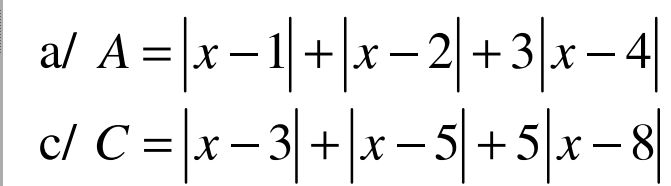
Tìm GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
a. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-4|=|x-1|+|4-x|\geq |x-1+4-x|=3$
$|x-2|+|x-4|=|x-2|+|4-x|\geq |x-2+4-x|=2$
$|x-4|\geq 0$
Cộng theo vế:
$A\geq 5$
Vậy $A_{\min}=5$. Giá trị này đạt tại \(\left\{\begin{matrix} (x-1)(4-x)\geq 0\\ (x-2)(4-x)\geq 0\\ x-4=0\end{matrix}\right.\Leftrightarrow x=4\)
Đúng 1
Bình luận (0)
c. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ thì:
$|x-3|+|x-8|=|x-3|+|8-x|\geq |x-3+8-x|=5$
$|x-5|+|x-8|=|x-5|+|8-x|\geq |x-5+8-x|=3$
$3|x-8|\geq 0$
Cộng theo vế:
$C\geq 8$. Vậy $C_{\min}=8$. Giá trị này đạt tại $x=8$
Đúng 1
Bình luận (0)
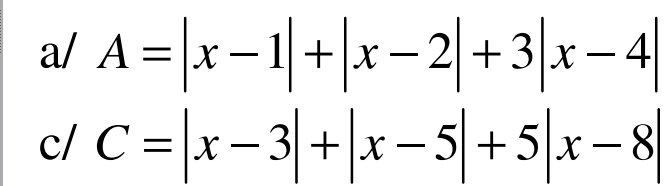
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
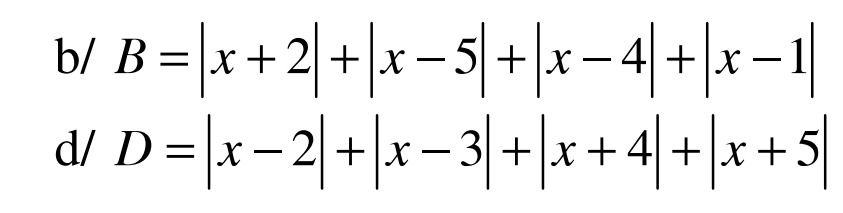
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
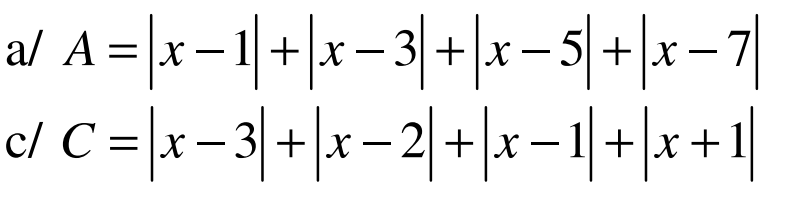
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
giải nhanh giúp mình với nhá
x : 0,5 + x : 0,125 = 10,35
nói luôn kết quả nhá, mình đang cần RẤT RẤT RẤT gấp đó

Mình đag cần rất rất gấp. mọi ng giúp mình với ak
ta có \(\left(x-4\right)\left(6-x\right)\le\left(\frac{x-4+6-x}{2}\right)^2=1\) (bất đẳng thức cauchy)
mà \(\left|y+1\right|\ge0\Rightarrow\left|y+1\right|+2\ge2>1\)
Vậy phương trình trên vô nghiệm
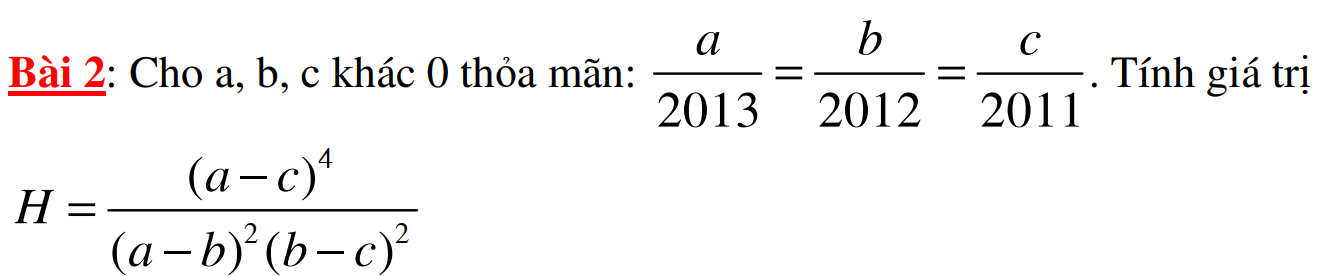
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak.
Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)
Đúng 3
Bình luận (0)















