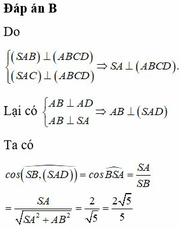Cho hình chóp S. ABCD có đáy là hình vuông góc với đáy ABCD. Tính góc giữa 2 mặt phẳng SAB và SAD

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng
S
A
B
v
à
S
A
C
là
60
°
;
góc giữa hai mặt phẳng
S
A
B...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng S A B v à S A C là 60 ° ; góc giữa hai mặt phẳng S A B v à S A D là 45 ° Gọi α là góc giữa hai mặt phẳng S A B v à A B C D , tính cos α
A. cos α = 1 2
B. cos α = 2 2
C. cos α = 3 2
D. cos α = 2 3
Phương pháp:
- Sử dụng phương pháp tọa độ trong không gian, gắn hệ trục tọa độ gốc A và các trục tọa độ sao cho

- Sử dụng các công thức điểm, véc tơ, mặt phẳng, góc giữa hai mặt phẳng để tính toán.
Cách giải:
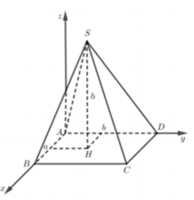
Gắn hệ trục tọa độ như hình vẽ, giả sử ABCD là hình vuông cạnh l,
chiều cao hình chóp SH = h.
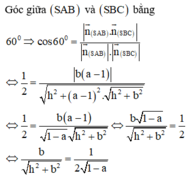
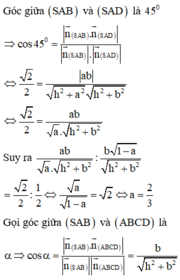
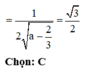
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA2
α
Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA=2 α Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
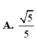
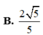
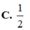
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) A.
5
5
B.
2
5
5
C.
1
2
D. 1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
A. 5 5
B. 2 5 5
C. 1 2
D. 1
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)? A.
5
5
B.
2
5
5
C.
1
2
D. 1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)?
A. 5 5
B. 2 5 5
C. 1 2
D. 1
Đáp án B

Vì ABCD là hình vuông ⇒ A B ⊥ A D 1
Ta có S A B ⊥ A B C D S A C ⊥ A B C D ⇒ S A ⊥ A B C D ⇒ S A ⊥ A B 2
Từ (1), (2) suy ra A B ⊥ S A D ⇒ S B ; S A D ^ = S B ; S A ^ = B S A ^
Tam giác SAB vuông tại A, có cos B S A ^ = S A S B = S A S A 2 + A B 2 = 2 5 5 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) . A.
5
5
B.
2
5
5
C.
1
2
D .1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) .
A. 5 5
B. 2 5 5
C. 1 2
D .1
Chọn B.
Phương pháp: Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm O, SA vuông góc mặt đáy, SA = aV3 . Tính góc giữa hai mặt phẳng: a) Góc ((SAB),(ABCD)), ((SAB),(SAD)).
a: (SAB) giao (ABCD)=AB
SA vuông góc AB, SA thuộc (SAB)
AD vuông góc AB, AD thuộc (ABCD)
=>((SAB);(ABCD))=góc SAD=90 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng
60
0
. Tính theo a khoảng cách giữa 2 đường thẳng SB,AD? A.
a
3
B.
a
3
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 60 0 . Tính theo a khoảng cách giữa 2 đường thẳng SB,AD?
A. a 3
B. a 3 2
C. a 3 3
D. a 3 5
Đáp án B
Hướng dẫn giải:
+)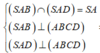
![]()
![]()
+) ![]()
![]()
+) Ta có A B ⊥ B C , kẻ A P ⊥ S B ( P ∈ S B )
d(A;(SBC)) = AP ⇒ d(AD;SB) = AP
+) 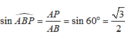
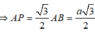
![]()
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB a, BC 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc
α
. Tính thể tích khối chóp S. ABCD theo
α
A.
2
a
3
15
3
B.
2
a
3...
Đọc tiếp
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB = a, BC= 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc α . Tính thể tích khối chóp S. ABCD theo α
A. 2 a 3 15 3
B. 2 a 3 15
C. 2 a 3
D. 2 a 3 15 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
60
0
. Tính theo a thể tích khối chóp S.ABCD A.
3
a
3
B.
a
3...
Đọc tiếp
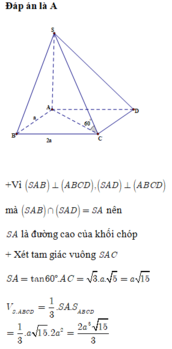
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 60 0 . Tính theo a thể tích khối chóp S.ABCD
A. 3 a 3
B. a 3 6 9
C. a 3 6 3
D. 3 2 a 3
Chọn đáp án C
Ta có
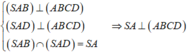
⇒ A C là hình chiếu của SC trên mặt phẳng (ABCD)
![]()
Lại có ABCD là hình vuông cạnh a nên A C = a 2
Tam giác SAC vuông tại A nên S A = A C . tan S C A ⏜ = a 6
Vậy thể tích khối chóp S.ABCD là V A B C D = a 3 6 3 (đvtt).
Đúng 0
Bình luận (0)