Cho t.gi ABC vuông tai A. Tinh dien tich t.gi ABC biet AB=5cm, AC=1/3BC.

Những câu hỏi liên quan
Cho tam giac ABC. M la trung diem cua cach BC .Tren AC lay diem N sao cho AN =1/4 AC tai diem . Noi diem MN keo dai cat canh AB tai diem Q . Noi Q voi C . Cho biet dien tich AQN =10 . Tinh dien tich ABC
Cho tam giac ABC . Tren canh AB lay diem M sao cho AM bang 1/3 AB . Tren canh AC lay diem N sao cho AN bang 1/3 AC . Noi B voi N , noi C voi M ; BN cat CM tai .So sanh dien tich ABN voi dien tich ACM, so sanh dien tich BMI voi CNI, tinh dien tich ABC , biet dien tich tu giac AMIN la 90 cm2
cho hinh thang ABCD. Day ab bang 1/3 day cd, doan ac cat bd tai o. tim dien tinh tam giac abc va abd biet dien tich hinh thang la 48 cm2
cho tam giac abc ,I tren ab ma ai=1/2 ib ,m la trung diem ac ,bm cat ci tai o .biet dien tich aom la 4cm.tinh dien tich abc ,chung to dien tich coa=1/2 dien tich cob
cho tam giac ABC vuong tai A . AB=30cm ; AC=40cm . Tren BC lay trung diem D . AE=1/3 AB . AD cat CE tai M .
a) tinh dien tich ABC .
b) so sanh dien tich AMC va AMB
c) tinh ti so dien tich AME va ABC
-- cac ban nhanh giup to cau c) nhe !!!!!!!!
cho tam giac ABC tren BC lay trung diem M ; tren AC lay diem N sao cho AN=1/4 AC. noi diem M voi N. keo dai MN va AB cat nhau tai P,noi P voi C.. cho biet dien tich cua APN la 10 cm2.
a) Tinh dien tich PNC
b) Tinhdien tich ABC.
c) Hay so sanh PN voi MN
Cho tam giac ABc. D la diem nam tren canh AB sao cho AD bang 2/3 AB. E la diem nam tren canh AC sao cho AE bang 2/3 Ac. Mot duong thang di qua cat doan thang DE tai I va cat BC tai M.
1/ Tinh dien tich tam giac ADE biet dien tich tam giac ABC la 900cm2.
2/ So sanh AI va AM
Cho tam giác ABC cân ở A, AB = AC = 6cm, BH = 5cm tinh dien tich tam giac ABC
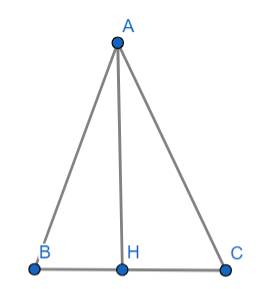
Xét tam giác vuông ABH vuông tại H ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)
\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)
Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)
Đúng 1
Bình luận (0)











