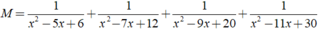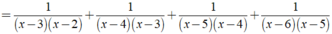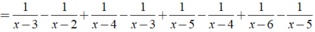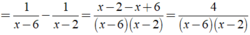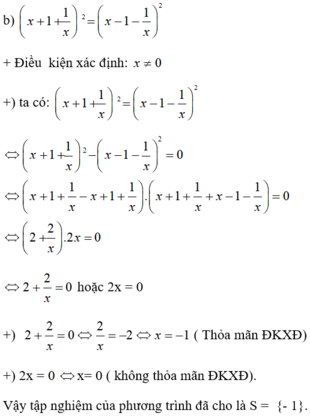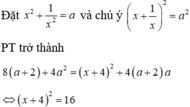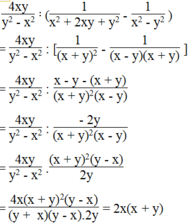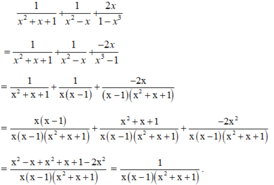1x2

Những câu hỏi liên quan
Tổng các nghiệm của phương trình:
1
x
2
+
4
x
+
3
+
1
x
2
+
8
x
+
15
+
1
x...
Đọc tiếp
Tổng các nghiệm của phương trình: 1 x 2 + 4 x + 3 + 1 x 2 + 8 x + 15 + 1 x 2 + 12 x + 35 + 1 x 2 + 16 x + 63 = 1 5 là
A. 10
B. -10
C. -11
D. 12
Áp dụng để rút gọn biểu thức sau:
M
1
x
2
-
5
x
+
6
+
1
x
2
-
7
x
+
12
+
1
x
2
-
9...
Đọc tiếp
Áp dụng để rút gọn biểu thức sau: M = 1 x 2 - 5 x + 6 + 1 x 2 - 7 x + 12 + 1 x 2 - 9 x + 20 + 1 x 2 - 11 x + 30
Biết
x
0
là nghiệm nhỏ nhất của phương trình
1
x
2
+
4
x
+
3
+
1
x
2
+
8
x...
Đọc tiếp
Biết x 0 là nghiệm nhỏ nhất của phương trình
1 x 2 + 4 x + 3 + 1 x 2 + 8 x + 15 + 1 x 2 + 12 x + 35 + 1 x 2 + 16 x + 63 = 1 5
Chọn khẳng định đúng.
A. x 0 > 0
B. x 0 < -5
C. x 0 = -10
D. x 0 > 5
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
Pt tương đương:
1 ( x + 1 ) ( x + 3 ) + 1 ( x + 3 ) ( x + 5 ) + 1 ( x + 5 ) ( x + 7 ) + 1 ( x + 7 ) ( x + 9 ) = 1 5
⇔ 2 ( x + 1 ) ( x + 3 ) + 2 ( x + 3 ) ( x + 5 ) + 2 ( x + 5 ) ( x + 7 ) + 2 ( x + 7 ) ( x + 9 ) = 2 5
ĐKXĐ: x ≠ -1; -3; -5; -7; -9
Khi đó:
<=> 1 x + 1 - 1 x + 3 + 1 x + 3 - 1 x + 5 + 1 x + 5 - 1 x + 7 + 1 x + 7 - 1 x + 9 = 2 5
<=> 1 x + 1 - 1 x + 9 = 2 5
<=> 1 ( x + 9 ) - 1 ( x + 1 ) ( x + 1 ) ( x + 9 ) = 2 ( x + 1 ) ( x + 9 ) 5 ( x + 1 ) ( x + 9 )
=> 5[x + 9 – (x + 1)] = 2(x + 1) (x + 9)
ó 5(x + 9 – x – 1) = 2 x 2 + 20x + 18
ó 2 x 2 + 20x – 22 = 0
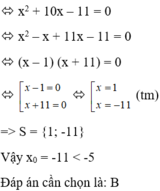
Đúng 0
Bình luận (0)
x3−1x2−x−x3+1x2+x
Bạn nên viết lại biểu thức bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) và ghi đầy đủ yêu cầu đề để mọi người hỗ trợ tốt hơn nhé.
Đúng 0
Bình luận (0)
Giải phương trình:
x
+
1
+
1
x
2
x
-
1
...
Đọc tiếp
Giải phương trình: x + 1 + 1 x 2 = x - 1 - 1 x 2
Rút gọn biểu thức:a)
P
1
(
x
−
2
y
)
2
+
1
x
2
−
4...
Đọc tiếp
Rút gọn biểu thức:
a) P = 1 ( x − 2 y ) 2 + 1 x 2 − 4 y 2 + 1 ( x + 2 y ) 2 . x 2 + 4 xy + 4 y 2 16 x
b) Q = 1 x 2 + 8 x + 16 − 1 x 2 − 8 x + 16 : 1 x + 4 + 1 x − 4 .
a) Ta có P = 4 x 2 ( x − 2 y ) 2 ( x + 2 y ) 2 . ( x + 2 y ) 2 16 x = x 4 ( x − 2 y ) 2
Với x ≠ 0 , x ≠ ± 2 y
b) Ta có Q = 16 x ( x 2 − 16 ) 2 . x 2 − 16 2 x = 8 16 − x 2 với x ≠ 0 , x ≠ ± 4
Đúng 0
Bình luận (0)
Giải phương trình:
8
x
+
1
x
2
+
4
x
2
+
1
x
2
2
x
+
4
2...
Đọc tiếp
Giải phương trình:
8 x + 1 x 2 + 4 x 2 + 1 x 2 2 = x + 4 2 + 4 x + 1 x 2 x 2 + 1 x 2
Thực hiện các phép tính sau:
4
x
y
y
2
-
x
2
:
1
x
2
+
2
x
y
+
y
2...
Đọc tiếp
Thực hiện các phép tính sau: 4 x y y 2 - x 2 : 1 x 2 + 2 x y + y 2 - 1 x 2 - y 2
Làm tính cộng các phân thức:
1
x
2
+
x
+
1
+
1
x
2
-
x
+
2
x
1
-
x
3
Đọc tiếp
Làm tính cộng các phân thức: 1 x 2 + x + 1 + 1 x 2 - x + 2 x 1 - x 3
Tìm m C2.Với
C
lim
x
→
1
x
2
−
m
x
+
m
−
1
x
2
−
1
để: A. m2 B. m -2 C. m1 D. m -1
Đọc tiếp
Tìm m C=2.Với C = lim x → 1 x 2 − m x + m − 1 x 2 − 1 để:
A. m=2
B. m= -2
C. m=1
D. m= -1
Đáp án là B
Ta có:
C = lim x → 1 x − 1 x + 1 − m x − 1 x − 1 x + 1 = lim x → 1 x + 1 − m x + 1 = 2 − m 2
mà C = 2 ⇒ m = − 2.
Đúng 0
Bình luận (0)