Cho hai điểm C , D nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆ACD=∆BCD

Những câu hỏi liên quan
Cho đoạn thẳng AB có M là trung điểm. Qua M kẻ đường thẳng d⊥AB. Trên d lấy C,D. Chứng minh :
a) AC = BC.
b) ▲ACD = ▲BCD.
cho đoạn thẳng AB. Qua trung điểm M của đoạn thẳng AB vẽ đường thẳng xy sao cho xy vuông góc AB, trên tia Mx lấy C và D sao cho C nằm giữa M và D. Trên tia My lấy điểm E. Chứng minh:
a) tam giác AMC=tam giác BMC
b)tam giác ACD=tam giác BCD
c) gócDAE=góc DBE
Cho hai điểm A và D nằm trên đường trung trực AI của đoạn thẳng BC, D nằm giữa hai điểm A và I, I là điểm nằm trên BC.
Chứng minh rằng:
a) AD là tia phân giác của góc BAC
b) Góc ABD = Góc ACD
Cho đoạn thẳng ab có m là trung điểm. Qua m kẻ đường thẳng d vuông góc ab. Trên (d) lấy các điểm C, D. Chứng minh:
a) AC = BC
b) Tam giác ACD = Tam giác BCD
Cho đoạn thẳng AB, M là trung điểm của AB ta kẻ đường thẳng xx' vuông góc với AB. trên tia Mx (xx' vuông góc với AB TẠI M) lấy hai điểm C và D sao cho C nằm giữa và D. Trên tia Mx, Lấy điểm E sao cho E khác M.
a) Chứng minh AC=BC
b) Tam giác ACD = tam giác BCD
c) góc EAD = góc EBD
Cho đoạn thẳng AB và đường thẳng d không vuông góc với nhau, đường thẳng d không cắt đoạn thẳng AB. Vẽ các điểm C,D sao cho đường thẳng d là trung trực các đoạn thẳng BC,AD. Hai đường thẳng BC và AD lần lượt cắt đường thẳng d tại I và K.Chứng minh rằng:Các đường thẳng AB và CD cắt nhau tại E nằm trên đường thẳng d.Giao điểm các đường trung trực từng tam giác BEC,AED nằm trên đường thẳng d.
Đọc tiếp
Cho đoạn thẳng AB và đường thẳng d không vuông góc với nhau, đường thẳng d không cắt đoạn thẳng AB. Vẽ các điểm C,D sao cho đường thẳng d là trung trực các đoạn thẳng BC,AD. Hai đường thẳng BC và AD lần lượt cắt đường thẳng d tại I và K.
Chứng minh rằng:
Các đường thẳng AB và CD cắt nhau tại E nằm trên đường thẳng d.Giao điểm các đường trung trực từng tam giác BEC,AED nằm trên đường thẳng d.Cho hai điểm A, D nằm trên đường trung trực của đoạn thẳng BC.
a) Chứng minh: tam giác ABD = tam giác ACD
b) Cho BC=12 cm; AB=7,5cm; DB=6,5cm. Tính AD trong hai trường hợp:
TH1: A,D cùng nằm trên nửa mặt phẳng bờ BC;
TH2: A,D không cùng nằm trên nửa mặt phẳng bờ BC.
pan lucy heartfilia oi ,pn cho mk di mk giai cho
Đúng 0
Bình luận (0)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
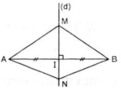
Vì M thuộc đường trung trực của AB
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm của đoạn BD.
a) Chứng minh tam giác BCD cân.
b) Gọi K là trung điểm BC. Đường thẳng DK cắt AC tại M. Chứng minh AM = 1/2.MC
c) Đường trung trực d của đoạn AC cắt DC tại Q. Chứng minh B, M, Q thẳng hàng.
Cú mìnhhh
a: Xét ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>AM=1/2MC
c: Gọi giao của d với AC là E
d là trung trực của AE
=>QE vuông góc AC tại E và E là trung điểm của AC
Xét ΔCAD có
E là trung điểm của CA
EQ//DA
=>Q là trung điểm của CD
Xét ΔCBD có
M là trọng tâm
BQ là đường trung tuyến
Do đó; B,Q,M thẳng hàng
Đúng 2
Bình luận (0)














