chứng minh rằng đường thẳng Mu //với đường thẳng Z biết NMu=150,MNT=120,NTz=90

Những câu hỏi liên quan
cho đường thẳng zz' cắt 2 đường thẳng yy' và xx' tại điểm A và B , sao cho góc z'AB= 60° và góc yBz=120°. chứng minh rằng : xx' // yy'
giúp với :((
cho đường thẳng zz' cắt 2 đường thẳng yy' và xx' tại điểm A và B , sao cho góc z'AB= 60° và góc yBz=120°. chứng minh rằng : xx' // yy'
Cho hình bs 12
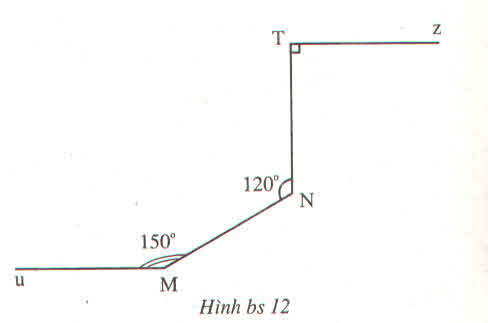
Chứng minh rằng đường thẳng Mu song song với đường thẳng Tz ?
Cho tam giác ABC cân tạo A ( góc BAC>90 độ). Đường thẳng qua B và vuông góc với AB cắt đường thẳng qua C và vuông góc với AC tại D
a) Chứng minh rằng AD là đường phân giác của tam giác ABC
b) Đường thẳng qua B và vuông góc với BC cắt đường thẳng CA tại E. Chứng minh rằng tam giác ABE cân và BA là đường trung tuyến của tam giác EBC
Cho góc xOy 90 độ. Trên tia phân giác của góc x Cho góc xOy 90 độ. Trên tia phân giác của góc xOy lấy điểm A. Qua A, kẻ đường thẳng vuông góc với Ox tại B và đường thẳng vuông góc với Oy tại C.a) Chứng minh OB OC.b)Chứng minh OA là đường trung trực của đoạn thẳng BC.c) Gọi D là giao điểm của đường thẳng AB với tia Oy, gọi E là giao điểm của đường thẳng AC với tia Ox. Chứng minh rằng: tam giác DOE cân.d) Chứng minh tứ giác BCDE là hình thang.Giúp mình với, huhuhuhuhu TvT
Đọc tiếp
Cho góc xOy < 90 độ. Trên tia phân giác của góc x Cho góc xOy < 90 độ. Trên tia phân giác của góc xOy lấy điểm A. Qua A, kẻ đường thẳng vuông góc với Ox tại B và đường thẳng vuông góc với Oy tại C.
a) Chứng minh OB = OC.
b)Chứng minh OA là đường trung trực của đoạn thẳng BC.
c) Gọi D là giao điểm của đường thẳng AB với tia Oy, gọi E là giao điểm của đường thẳng AC với tia Ox. Chứng minh rằng: tam giác DOE cân.
d) Chứng minh tứ giác BCDE là hình thang.
Giúp mình với, huhuhuhuhu TvT
Cho hình bình hành ABCD với
B
A
D
^
90
∘
.Đường phân giác của góc
B
C
D
^
cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.Kẻ đường thẳng d đi qua A và vuông góc với CO.Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại...
Đọc tiếp
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
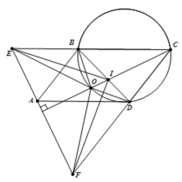
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
![]() .
.
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD với
B
A
D
^
90
∘
.Đường phân giác của góc
B
C
D
^
cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.Kẻ đường thẳng d đi qua A và vuông góc với CO.Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại...
Đọc tiếp
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
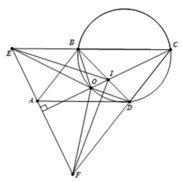
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác ![]() .
.
Đúng 0
Bình luận (0)
Cho Tam Giác ABC, có BAC =120 đọ. đường phân giác trong của góc A cắt BC tại D.Từ D kẻ DE vuông góc với AB, DF vuông góc với AC.a)Chứng MInh tam giác ADE = ADF. b)Chứng minh rằng tam giác DEF là tam giác đều C) qua điểm C vẽ đường thẳng song song với AD, nó cắt đường thẳng AB tại M. Chứng minh rằng tam giác ACM là tam giác đèu
Cho hình bình hành ABCD với
B
A
D
^
90
∘
.Đường phân giác của góc
B
C
D
^
cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.Kẻ đường thẳng d đi qua A và vuông góc với CO.Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại...
Đọc tiếp
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
1). Chứng minh rằng Δ O B E = Δ O D C .
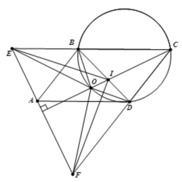
1). Tứ giác OBCD nội tiếp và CO là phân giác góc B C D ^ , suy ra O B D ^ = O C D ^ = O C B ^ = O D B ^ , nên tam giác OBD cân tại O, do đó OB=OD (1).
Tứ giác OBCD nội tiếp O D C ^ = O B E ^ (cùng bù với góc OBC) (2).
Trong tam giác CEF có CO vừa là đường cao vừa là đường phân giác nên tam giác CEF cân tại ![]() .
.
Do A B ∥ C F ⇒ A E B ^ = A F C ^ = E A B ^ , suy ra tam giác ABE cân tại B, nên B E = B A = C D ( 3 )
Đúng 0
Bình luận (0)











