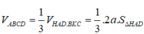cho nửa đường tròn tâm O , đường kính AD=8. Trên nửa mặt phẳng đường tròn đó , lấy B và C sao cho tứ giác ABCD có AB=BC=2. Gọi CD là x. Tính CD ?

Những câu hỏi liên quan
Cho đường tròn tâm O, đường kính AB, M là một điểm thuộc nửa đường tròn. Qua M vẽ vẽ tiếp tuyến với nửa đường tròn, gọi D và C theo thứ tự là các hình chiếu vuông góc của A và B.a) Chứng minh M là trung điểm của CD b) Chứng minh AB BC + ADc) Giả sử góc AOM góc BOM. Từ B vẽ đường tròn vuông góc với BC, đường thẳng này cắt AD tại E. Chứng minh E thuộc nửa đường tròn tâm O d) Xác định vị trí của M trên 1/2 O sao cho tứ giác ABCD có diện tích lớn nhất và tính diện tích đó theo nửa bán kính rồi the...
Đọc tiếp
Cho đường tròn tâm O, đường kính AB, M là một điểm thuộc nửa đường tròn. Qua M vẽ vẽ tiếp tuyến với nửa đường tròn, gọi D và C theo thứ tự là các hình chiếu vuông góc của A và B.
a) Chứng minh M là trung điểm của CD
b) Chứng minh AB = BC + AD
c) Giả sử góc AOM > góc BOM. Từ B vẽ đường tròn vuông góc với BC, đường thẳng này cắt AD tại E. Chứng minh E thuộc nửa đường tròn tâm O
d) Xác định vị trí của M trên 1/2 O sao cho tứ giác ABCD có diện tích lớn nhất và tính diện tích đó theo nửa bán kính rồi theo 1/2 đường tròn đã cho.
Giúp em với ạ TvT
Cho đường tròn tâm O đường kính AB 2R. Trên nửa mặt phẳng bờ AB vẽ các tiếp tuyến Ax, By. Trên Ax lấy C, trên By lấy D sao cho góc COD 90 độChứng minh:a) CD AC + BD (đã làm được)b)CD là tiếp tuyến của đường tròn đường kính AB (M là tiếp điểm)c) AC.BD không đổi khi C và D di độngd) AB là tiếp tuyến của đường tròn đường kính CDe) Gọi N là giao điểm của AD và BC. Chứng Minh MN//AC
Đọc tiếp
Cho đường tròn tâm O đường kính AB = 2R. Trên nửa mặt phẳng bờ AB vẽ các tiếp tuyến Ax, By. Trên Ax lấy C, trên By lấy D sao cho góc COD = 90 độ
Chứng minh:
a) CD = AC + BD (đã làm được)
b)CD là tiếp tuyến của đường tròn đường kính AB (M là tiếp điểm)
c) AC.BD không đổi khi C và D di động
d) AB là tiếp tuyến của đường tròn đường kính CD
e) Gọi N là giao điểm của AD và BC. Chứng Minh MN//AC
CHO Tam giác abc đều trên nửa mặt phẳng bờ bc không chứa điểm a vẽ nửa đường tròn đường kính bc. lấy điểm d thuộc nửa đường tròn sao cho sd CD = 60. gọi i là giao điểm ad và bc. chứng minh bi=2ci
Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy B,C sao cho AB=BC= 2√5 cm, CD=6cm. Tính bán kính của (O
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2 TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
Đọc tiếp
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2= TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)
b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)
\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)
c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)
mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)
mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)
Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)
\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Từ 1 điểm M nằm trên nửa đường tròn vẽ tiếp tuyến xy. Vẽ AD và BC cùng vuông góc với xy.
C/m MC=MDC/m AD+BC có giá trị không đổi khi M di chuyển trên nửa đường tròn.C/m AD là tiếp tuyến của đường tròn đường kính CD.Xác định vị trí của M trên nửa đường tròn để diện tích tứ giác ABCD lớn nhất.1. Ta có AD // OM // BC ; OA = OB
=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD
2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi.
3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD
Lại có AD vuông góc với MD => đpcm
4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)
Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB
Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R2 với R = AB/2
Đúng 1
Bình luận (4)
Cho nửa đường tròn (O) đường kính AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. Điểm M nằm trên (O) sao cho tiếp tuyến tại M cắt Ax, By tại D và C. Chứng minh:a, AD + BC CDb,
C
O
D
^
90
0
c, AC.BD
O
A...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. Điểm M nằm trên (O) sao cho tiếp tuyến tại M cắt Ax, By tại D và C. Chứng minh:
a, AD + BC = CD
b, C O D ^ = 90 0
c, AC.BD = O A 2
d, AB là tiếp tuyến của đường tròn đường kính CD
Sử dụng tính chất hai tiếp tuyến
a, Ta có: AC = CM; BD = DM => AC+BD=CD
b, C O A ^ = C O M ^ ; D O M ^ = D O B ^
=> C O D ^ = 90 0
c, AC.BD = MC.MD = M O 2 = R 2
d, Gọi I là trung điểm của CD. Sử dụng tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông và đường trung bình trong hình thang để suy ra đpcm
Đúng 0
Bình luận (0)
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho
A
D
2
3
a
; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt
α
là...
Đọc tiếp
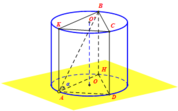
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho A D = 2 3 a ; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt α là góc giữa AB và đáy. Tính tan α khi thể tích khối tứ diện CDAB đạt giá trị lớn nhất.
A. tan α = 3
B. tan α = 1 2
C. tan α = 1
D. tan α = 3 3
cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng bờ AB có chứa nửa đường tròn vẽ tia Ax vuông góc AB. Lấy điểm C trên nửa đường tròn rồi vẽ tia phân giác góc ABC cắt nửa đường tròn tại điểm thứ 2 là D và cắt tia Ax, AC lần lượt tại E và H.. AD cắt BC tại F.
cm: FH vuông góc AB ; AEFH là hình gì ; CHo biết AB=2R, góc ABC=60độ, tính diện tích tứ giác AEFH?