Một tấm bìa hình chữ nhật có kích thước 60cm;96cm.hãy cắt tấm bìa hình chữ nhật có kích thước 60cm;96cm hãy cắt tấm bìa dài là cạnh lớn nhất .tính độ dài cạnh lớn nhất đó

Những câu hỏi liên quan
Bạn Hoa muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 960cm thành các mảnh nhỏ hình vuông sao cho tấm bìa được cắt hết, không thừa không thiếu. Tính độ dài lớn nhất của cạnh hình vuông.
Xem chi tiết
ta có bội chung nhỏ nhất của 60 và 960 là
BCNN(60,960) = 60
thế nên cạnh hình vuông lớn nhất có thể là 60cm
Hùng cắt 1 tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Độ dài lớn nhất của cạnh hình vuông là ..... cm?
Xem chi tiết
Vì tấm bìa được cắt hết => cạnh của hình vuông là ước chung của chiều dài và chiều rộng hình chữ nhật.
Khi đó độ dài cạnh hình vuông lớn nhất chính là ƯCLN của chiều dài và chiều rộng hình chữ nhật.
Ta có: 60 = 22.3.5
96 = 25.3
ƯCLN(60;96) = 22.3 = 12
Cạnh hình vuông là 12 cm
Đúng 0
Bình luận (0)
Diện tích tấm bìa hình chữ nhật là 96 x 60 = \(5760\left(cm^2\right)\)
Để cắt tấm bìa thành a mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết và cạnh hình vuông có độ dài lớn nhất là b (cm) thì a phải là số nhỏ nhất sao cho \(5760:a=b^2\)
Mà \(5760=2^7.3^2.5=\left(2^6.3^2\right).\left(2.5\right)\)
\(=\left(8^2.3^2\right).10=24^2.10\)
Nên khi số mảnh lớn nhất là a = 10 thì cạnh hình vuông có độ dài lớn nhất là 24 cm
\(5760=24^2.10\)
\(5760=24^2.10\)
Đúng 0
Bình luận (0)
Hùng muốn cắt 1 tấm bìa hình chữ nhật có kích thước 60cm, 90cmchia thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Tính độ dài lớn nhất của cạnh hình vuông
Độ dài lớn nhất của cạnh hình vuông là 30cm
Đúng 0
Bình luận (0)
Ta có :
90 = 2.32.5
60 = 22.5.3
Vậy ƯCLN của 60 và 90 là :
2.3.5 = 30
Suy ra cạnh của hình vuông lớn nhất có thể là 30 cm
Đáp số : 30 cm
Đúng 0
Bình luận (0)
90 = 2 . 32 . 5
60= 22.3.5
=> ƯCNN(60;90)=30
=> đọ dài lớn nhất của ình vuông là:
30 cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông băng nhau sao cho tấm bìa được cắt hết.Tính độ dài lớn nhất của cạnh hình vuông [số đo cạnh hình vuông nhỏ là một số tự nhiên với đơn vị là xentimét]
Diện tích mảnh bìa :
60 x 96 = 5760 ( cm2 )
các số là bội của 5760 :
1 , 2 , 3 , 4 , 6 ,10 , 576 , ........
Số lớn nhất trong các số đó là 576 , vậy độ dài lớn nhất của cạnh hình vuông :
576 \(:\sqrt{576}=24\left(cm\right)\)
đ/s : 24 cm
Đúng 0
Bình luận (0)
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 90cm thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Tính độ dài lớn nhất của cạnh hình vuông (số đo cạnh của hình vuông nhỏ là một số tự nhiên với đơn vị là xentimet)?
Gọi a (cm) là độ dài lớn nhất của cạnh hình vuông. Theo đề bài thì a = ƯCLN(60,90)
Vậy a = 30 cm
Đúng 0
Bình luận (0)
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 90cm thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Tính độ dài lớn nhất của cạnh hình vuông (số đo cạnh của hình vuông nhỏ là một số tự nhiên với đơn vị là xentimet)?
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Tính độ dài lớn nhất của cạnh hình vuông (số đo của hình vuông nhỏ là một số tự nhiên với đơn vị là xen ti mét)
Vì tấm bìa được cắt hết nên cạnh của hình vuông là ước chung của chiều dài và chiều rộng hình chữ nhật. Khi đó độ dài cạnh hình vuông lớn nhất chính là ƯCLN của chiều dài và chiều rộng hình chữ nhật. Ta có: 60 = 22.3.5; 96 = 25.3
ƯCLN(60;96) = 22.3 = 12
Vậy cạnh hình vuông lớn nhất bằng 12 cm
Đúng 0
Bình luận (0)
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết. Tính độ dài lớn nhất của cạnh hình vuông (số đo của hình vuông nhỏ là một số tự nhiên với đơn vị là xen ti mét)
Vì tấm bìa được cắt hết nên cạnh của hình vuông là ước chung của chiều dài và chiều rộng hình chữ nhật. Khi đó độ dài cạnh hình vuông lớn nhất chính là ƯCLN của chiều dài và chiều rộng hình chữ nhật
Ta có: 60=2^2.3.5
96=2^5.3
ƯCLN(60; 96) =2^2.3=12
Vậy độ dài lớn nhất của cạnh hình vuông là 12 cm.
~ HT ~
Trong một hộp có chứa các tấm bìa dạng hình chữ nhật có kích thước đôi một khác nhau, các cạnh của hình chữ nhật có kích thước là m và n (
m
,
n
∈
N
;
1
≤
m
,
n
≤
20
,
đơn vị là cm). Biết rằng mỗi bộ kích thước ( m,n) đều có tấm bìa tương ứng. Ta gọi một tấm bìa là “tốt” nếu tấm bìa đó có thể được lắp ghép từ các miếng bìa dạng hình chữ L gồm 4 ô vuông, mỗi ô có độ dài cạnh l...
Đọc tiếp
Trong một hộp có chứa các tấm bìa dạng hình chữ nhật có kích thước đôi một khác nhau, các cạnh của hình chữ nhật có kích thước là m và n ( m , n ∈ N ; 1 ≤ m , n ≤ 20 , đơn vị là cm). Biết rằng mỗi bộ kích thước ( m,n) đều có tấm bìa tương ứng. Ta gọi một tấm bìa là “tốt” nếu tấm bìa đó có thể được lắp ghép từ các miếng bìa dạng hình chữ L gồm 4 ô vuông, mỗi ô có độ dài cạnh là 1cm để tạo thành nó (Xem hình vẽ minh họa một tấm bìa “tốt” bên dưới) .
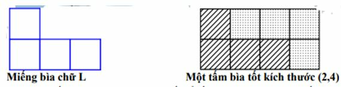
Rút ngẫu nhiên một tấm bìa từ hộp, tính xác suất để tấm bìa vừa rút được là tấm bìa “tốt”
A. 29/95
B. 2/7
C. 29/105
D. 9/35




















