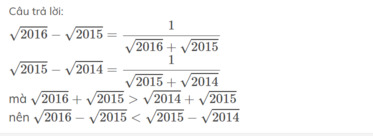so sanh 2014/2015 va 2015/2016

Những câu hỏi liên quan
2015/-2014 va -2016/2015 . So sanh]
\(\frac{2015}{-2014}\)>\(\frac{-2016}{2015}\)
Đúng 0
Bình luận (0)
so sanh a va b a=2014+2015/2015+2016vab=2015+2016/2016+2017
Giải:
Ta có:
\(A=\frac{2014+2015}{2015+2016}=\frac{2014+2015+2}{2015+2016}-\frac{2}{2015+2016}=2-\frac{2}{2015+2016}\)(1)
\(B=\frac{2015+2016}{2016+2017}=\frac{2015+2016+2}{2016+2017}-\frac{2}{2016+2017}=2-\frac{2}{2016+2017}\)(2)
Từ (1) và (2) ta có: \(A=2-\frac{2}{2015+2016}\)và \(B=2-\frac{2}{2016+2017}\)
Vì \(\frac{2}{2015+2016}>\frac{2}{2016+2017}\rightarrow2-\frac{2}{2015+2016}< 2-\frac{2}{2016+2017}\)
\(\Rightarrow A< B\)
Đúng 0
Bình luận (0)
so sanh a=2004^2016+1/2004^2015+1 va b=2004^2015+1/2004^2014+1
So sanh : \(\sqrt{2016}-\sqrt{2015}va\sqrt{\sqrt{2015}-}\sqrt{2014}\)
cho A= 2015^2014+1 phần 2015^2016+1
B=2015^2015+1 phan 2015^2016+1
so sanh A va B
GIÚP MÌNH VỚI MAI NỘP RỒI !!!
Ta có 20152015 = 20152015
Ta so sánh 20152016+1 và 20152011+1
Vì 20152016 > 20152011
=> 20152016+1 > 20152011 +1
2 phân số có cùng tử số, mẫu của phân số nào nhỏ hơn thì phân số đó lớn hơn
=> A < B
Đúng 0
Bình luận (0)
Ta có 20152015 = 20152015
Ta so sánh 20152016+1 và 20152011+1
Vì 20152016 > 20152011
=> 20152016+1 > 20152011 +1
2 phân số có cùng tử số, mẫu của phân số nào nhỏ hơn thì phân số đó lớn hơn
=> A < B
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tinh A= 2014/2015+2015/2016+2016/2017+2017/2014 hay so sanh A voi 4
=(2014/2014)+(2015+2015)+(2016/2016)+(2017+2017)
=1+1+1+1
=4
vậy A=4 (4=4)
Đúng 0
Bình luận (0)
so sanh a= 2015^2014+1/2015^2014-1 va b= 2015^2014-1/2015^2014-3
\(A=\frac{2015^{2014}+1}{2015^{2014}-1}=\frac{2015^{2014}-1+2}{2015^{2014}-1}=1+\frac{2}{2015^{2014}-1}.\)
\(B=\frac{2015^{2014}-1}{2015^{2014}-3}=\frac{2015^{2014}-3+2}{2015^{2014}-3}=1+\frac{2}{2015^{2014}-3}\)
mà \(\frac{2}{2015^{2014}-1}< \frac{2}{2015^{2014}-3}\)( 20152014 -1 > 20152014 - 3)
\(\Rightarrow A< B\)
Đúng 0
Bình luận (0)
So sanh
A=2015^2015 + 1/ 2016^2016 + 1
B=2015^2014 + 1/ 2015^2015 + 1
Bạn lên mạng sear nha có đấy
Đúng 0
Bình luận (0)
So sanh tong sau voi 1
B=2014*2016+2000\2015*2015+1999
Ai tra loi dung va nhanh minh se tick
\(B=\frac{2014x2016+2000}{2015x2015+1999}\)
\(B=\frac{2014x2015+(2014+2000)}{2014x2015+(2015+1999)}\)
\(B=\frac{2014x2015+4014}{2014x2015+4014}=1\)
=> B = 1
Đúng 0
Bình luận (0)