Cho tam giác ABC, O là tâm đường tròn ngoại tiếp. Đường cao xuất phát từ A và B cắt
nhau tại H. Gọi M là trung điểm BC. CMR: AH = 2OM.

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O) có các đường cai AD, BE, CF cắt nhau tại H. Gọi M là trung điểm BC. (Mỗi ý có thể vẽ 1 hình khác nhau nếu cần thiêt)a) CMR H là tâm đường tròn nội tiếp tam giác DEb) CMR: AH 2OMc) Gọi H’ đối xứng với H qua đường thẳng BC. CMR: H’ thuộc đường tròn (O)d) CMR: đường tròn ngoại tiếp tam giác (BHC) đối xứng với đường tròn qua đường thẳng BC.
Đọc tiếp
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O) có các đường cai AD, BE, CF cắt nhau tại H. Gọi M là trung điểm BC. (Mỗi ý có thể vẽ 1 hình khác nhau nếu cần thiêt)
a) CMR H là tâm đường tròn nội tiếp tam giác DE
b) CMR: AH = 2OM
c) Gọi H’ đối xứng với H qua đường thẳng BC. CMR: H’ thuộc đường tròn (O)
d) CMR: đường tròn ngoại tiếp tam giác (BHC) đối xứng với đường tròn qua đường thẳng BC.
Cho tam giác ABC có các góc là góc nhọn và nội tiếp đường tròn tâm (O). Tiếp tuyến của đường tròn tâm (O) tại B,C cắt nhau tại D
a) Chứng minh OCDB nội tiếp
b) Gọi H là trực tâm của tam giác ABC. M là trung điểm của BC
Chứng minh AH=2OM
a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AH = 2OM
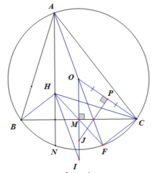
a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn nội tiếp đường tròn (O;R) , 2 đường cao BE và CF của tam giác ABC cắt nhau tại H . đường thẳng AH cắt BD tại D và cắt (O;R) tại điểm M a, chứng minh BC là p/g góc EMB b, gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF . chứng minh IE là tiếp tuyến của đường tròn ngoại tiếp tam giác BCE c, khi 2 điểm B,C cố định và điểm A di động trên (O;R) nhứng vẫn thỏa mãn tam giác ABC nhọn . chứng minh OA vuông góc với EF . xác định vị trí A để tổng DE+EF+FD đtặ giá trị nhỏ nhất
Đọc tiếp
cho tam giác ABC nhọn nội tiếp đường tròn (O;R) , 2 đường cao BE và CF của tam giác ABC cắt nhau tại H . đường thẳng AH cắt BD tại D và cắt (O;R) tại điểm M
a, chứng minh BC là p/g góc EMB
b, gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF . chứng minh IE là tiếp tuyến của đường tròn ngoại tiếp tam giác BCE
c, khi 2 điểm B,C cố định và điểm A di động trên (O;R) nhứng vẫn thỏa mãn tam giác ABC nhọn . chứng minh OA vuông góc với EF . xác định vị trí A để tổng DE+EF+FD đtặ giá trị nhỏ nhất
llllllllllllllllllllllllllllllllllllllllllllllllllllllllllloooooooooooooooonnnnnnnnnnnnnnnnnn
Vì 1 + 1 = 2 nên 2 + 2 = 4
Đáp số : Không Biết
Cho tam giác ABC cân tại A , các đương cao AD và BE cắt nhau tại H . Gọi O là tâm đường tròn ngoại tiếp tam giác AHE . CMR:
1) Bốn điểm : C,D,E,H cùng thuộc một đường tròn . Xác định tâm của đường tròn đó
2) BC=2DE
3) DE là tiếp tuyến của đường tròn (O)
Mọi người giải giúp mình với nha !
Cho tam giác nhọn ABC có AB AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Đọc tiếp
Cho tam giác nhọn ABC có AB < AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Ai giúp em với😢
Cho tam giác ABC, gọi H, G, O lần lượt là trực tâm, trọng tâm, tâm đường tròn ngoại tiếp của tam giác, M là trung điểm BC
a. CMR : AH = 2* OG
b> CMR : H, G, O thẳng hàng và GH= 2*OG
AI LÀM ĐÚNG MÌNH LIKE CHO
Cho tam giác ABC có các đường cao AD, BE, CF cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. M là trung điểm của BC. a) Chứng minh 4 điểm B, F, E, C cùng thuộc một đường tròn. Xác định tâm của đường tròn đó. b) Chứng minh tam giác AEF và tam giác ABC đồng dạng. c) Chứng minh OM = 1/2 AH
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân
Đọc tiếp
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE
2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân















