Cho S1=1.2.3
S2=2.3.4
S3=3.4.5
...
Sn=n(n+1)(n+2)
S=S1+S2+S3+...+Sn
Chứng minh:4S+1 là số chính phương
Những câu hỏi liên quan
cho tổng
S
n
1
1
.
2
+
1
2
.
3
+
.
.
.
+
1
n
n
+...
Đọc tiếp
cho tổng S n = 1 1 . 2 + 1 2 . 3 + . . . + 1 n n + 1 với n ∈ N *
a.Tính S1, S2, S3
b.Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
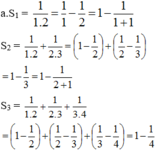
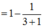
b. Dự đoán: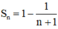 
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
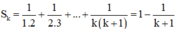
Khi đó:
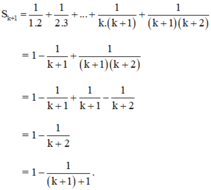
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
Đúng 0
Bình luận (0)
Cho hình nón (N) có góc ở đỉnh bằng 600 độ dài đường sinh bằng a. Dãy hình cầu (S1), (S2), (S3),… (Sn) thỏa mãn: (S1) tiếp xúc với mặt đáy và các đường sinh của hình nón (N) ; (S2) tiếp xúc ngoài với (S3) và tiếp xúc với các đường sinh của hình nón (N), (S3) tiếp xúc ngoài với (S2) và tiếp xúc với các đường sinh của hình nón (N). Tính tổng thể tích các khối cầu (S1), (S2), (S3),… (Sn) theo a.
Đọc tiếp
Cho hình nón (N) có góc ở đỉnh bằng 600 độ dài đường sinh bằng a. Dãy hình cầu (S1), (S2), (S3),… (Sn) thỏa mãn: (S1) tiếp xúc với mặt đáy và các đường sinh của hình nón (N) ; (S2) tiếp xúc ngoài với (S3) và tiếp xúc với các đường sinh của hình nón (N), (S3) tiếp xúc ngoài với (S2) và tiếp xúc với các đường sinh của hình nón (N). Tính tổng thể tích các khối cầu (S1), (S2), (S3),… (Sn) theo a.
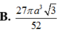
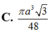
Gọi Sn là tổng các số tự nhiên n. Tính tổng: S1+S2+S3+...+S2012+S2013
Ta có:
S1 + S2 + S3 + ... + S2012 + S2013
= S( 1 + 2 + 3 + ... + 2012 + 2013 )
Đặt A = 1 + 2 + 3 + ... + 2012 + 2013
A = 2013 + 2012 + 2011 + ... + 1
2A = ( 1 + 2013 ) + ( 2 + 2012 ) + ( 3 + 2011 ) + ... ( 2013 + 1 ) ( 2013 cặp số )
2A = 2014 + 2014 + 2014 + ... + 2014 ( 2013 số 2014 )
2A = 2014 . 2013
2A = 4054182
A = 2027091
\(\Rightarrow\) Tổng S1 + S2 + S3 + ... + S2012 + S2013 là S2027091
Đúng 1
Bình luận (0)
Một vật dao động điều hoà với chu kì T6s. Gọi
s
1
,
s
2
,
s
3
lần lượt là ba quãng đường liên tiếp mà vật đi được trong thời gian 1 s, 2 s và 3 s kể từ lúc bắt đầu dao động. Biết tỉ lệ
s
1
:
s
2
:
s
3...
Đọc tiếp
Một vật dao động điều hoà với chu kì T=6s. Gọi s 1 , s 2 , s 3 lần lượt là ba quãng đường liên tiếp mà vật đi được trong thời gian 1 s, 2 s và 3 s kể từ lúc bắt đầu dao động. Biết tỉ lệ s 1 : s 2 : s 3 = 1 : 3 : n (với n là hằng số dương). Giá trị của n bằng
A. 4.
B. 7.
C. 6.
D. 5.
đặt S1=1+1/5;
S2=1+1/5+1/52
S3=1+1/5+1/52+1/53
.....
Sn=1+1/5+1/52+...+1/5n
chứng minh rằng 1/5(S1)2+1/52(S2)2+.......+1/5n(Sn)2<35/36
Cho tổng:
S
n
1
1
.
5
+
1
5
.
9
+
.
.
.
+
1
4
n
-...
Đọc tiếp
Cho tổng: S n = 1 1 . 5 + 1 5 . 9 + . . . + 1 4 n - 3 4 n + 1
a) Tính S 1 , S 2 , S 3 , S 4 ;
b) Dự đoán công thức tính S n và chứng minh bằng phương pháp quy nạp.
Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích
S
1
tiếp tục quá trình trên với các hình vuông với diện tích là
S
1
;
S
3
;
.
.
.
;
S
n
;
.
.
.
Tính tổng vô hạn
S
1...
Đọc tiếp
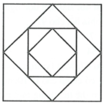
Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích S 1 tiếp tục quá trình trên với các hình vuông với diện tích là S 1 ; S 3 ; . . . ; S n ; . . . Tính tổng vô hạn S 1 + S 2 + S 3 + . . . + S n + . . .
A. 1
B. 1/2
C. 2
D. 3/2
cho a b c thuoc n sao va x+y+z=5; s1= b/a.x+c/a.z;s2=a/b.x+c/d.y;s3=a/c.z+b/c.y Chung minh s lon hon hoac bang 10 voi S=s1+s2+s3
mình ko biết, mới lớp 5 thui
đâu hàng 2 tay 2 chân
Đúng 0
Bình luận (0)
zậy hả vậy em nhỏ hơn chị 1 tuổi, học trường nào zay
Đúng 0
Bình luận (0)
cho tứ giác abcd có 2 đường chéo giao nhau tại o gọi s1 , s2 , s3 ,s4 lần lượt là diện tích các tam giác AOB , BOC , COD , DOA
a) CM s1=s2=s3=s4
b)Biết S1,s2,s3,s4 là các số nguyên dương . CM s1,s2,s3,s4 là số chính phương ( từ b,d kẻ đường vuông góc với ac)
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu
(
S
1
)
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
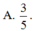
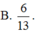
