DE là đường trung bình trong tam giác AHB nên DE // AB nên DE vuông góc AC

trong tam giác ADC có 2 đường cao ah de nên E là trực tâm nên CE vuông góc với AD

Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath

ảo à

đéo chứng minh được nhé

tự vẽ hình kiểm chứng đi

t.i.c.k mik mik t.i.c.k lại

1 phần thôi nhé

Nối BE, Gọi P là giao điểm của AD với BE.

Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).

Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)

Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)

Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác).  (4)

Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB

<=>  BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC  

<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5) 

    Chú ý: Ta cm được: CA=CD (biến đổi góc).

Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)

=> DpCm. 

a: Xét tứ giác ADHE có 

\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)

Do đó: ADHE là hình chữ nhật

Suy ra: AH=DE

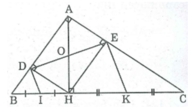
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH

⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)

⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0  - 2. ∠ B (1)

Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.

⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .

⇒  ∆ KHE cân tại K ⇒  ∠ (EKH) =  180 0 - 2. ∠ (KHE) (2)

Tứ giác ADHE là hình chữ nhật nên:

HE // AD hay HE // AB ⇒  ∠ B =  ∠ (KHE) (đồng vị)

Từ (1), (2) và (3) suy ra:  ∠ (DIB) =  ∠ (EKH)

Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).