em cảm ơn rất nhiều khi ac giúp e ạ

Những câu hỏi liên quan
ac giúp e với ạ em cảm ơn rất nhiều :((
ac giúp e với ạ e cảm ơn rất nhiều
Gọi chiều rộng, chiều dài lần lượt là a,b
Theo đề, ta có hệ phương trình:
a=1/4b và a(b+3)=ab+108
=>a=1/4b và 3a=108
=>a=36 và b=144
Đúng 0
Bình luận (0)
các ac giúp e với ạ. e cảm ơn rất nhiều
các ac giúp e với ạ e cảm ơn rất nhiều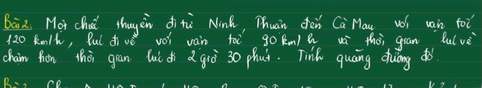
Gọi độ dài quãng đường là x
Thời gian đi là x/120(h)
Thời gian về là x/90(h)
Theo đề, ta có phương trình:
x/90-x/120=2,5
hay x=900
Đúng 0
Bình luận (0)
các ac giúp e với ạ e cảm ơn rất nhiều :((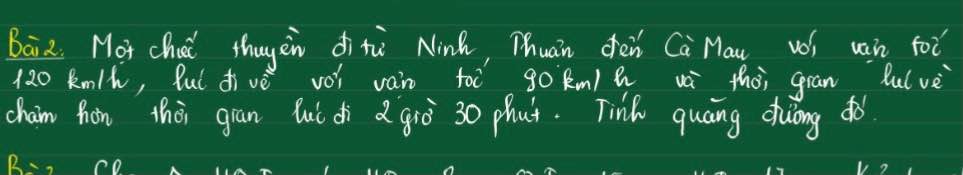
Gọi độ dài quãng đường là x
Thời gian đi là x/120(h)
Thời gian về là x/90(h)
Theo đề, ta có phương trình:
x/90-x/120=2,5
hay x=900
Đúng 0
Bình luận (0)
các ac giúp e với ạ e cảm ơn rất nhiều
các ac giúp e với ạ, e cảm ơn rất nhiều
tìm 5 phân số nằm giữa 5/7 và 6/7
ac giải chi tiết giúp e nha em cảm ơn ac rất nhiều ạ
\(\dfrac{5}{7}=\dfrac{30}{42};\dfrac{6}{7}=\dfrac{36}{42}. Vay5phansocantimla:\dfrac{31}{42};\dfrac{32}{42};\dfrac{33}{42};\dfrac{34}{42};\dfrac{35}{42}\)
Đúng 1
Bình luận (0)
Qui đồng 2 phân số lên ta có:
5/7 = 30/42 và 6/7 = 36/42
Vậy phân số nằm giữa là: 31/42 ; 32/42; 33/42; 34/42; 35/42
Đúng 1
Bình luận (0)
các ac giúp e dc k ạ, e cảm ơn rất nhiều
a.Áp dụng định lý pitago vào tam giác vuông PKQ, ta có:
\(QK^2=PQ^2+PK^2\)
\(\Rightarrow QK=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
Áp dụng t/c đường phân giác góc P, ta có:
\(\dfrac{PQ}{PK}=\dfrac{AP}{AK}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{3}{4}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{AK}{4}=\dfrac{AP}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{AK}{4}=\dfrac{AP}{3}=\dfrac{AK+AP}{4+3}=\dfrac{QK}{7}=\dfrac{10}{7}\)
\(\Rightarrow AK=\dfrac{10}{7}.4=\dfrac{40}{7}cm\)
\(\Rightarrow AP=\dfrac{10}{7}.3=\dfrac{30}{7}cm\)
b. Xét tam giác PBQ và tam giác PQK, có:
\(\widehat{PBQ}=\widehat{QPK}=90^0\)
\(\widehat{Q}:chung\)
Vậy tam giác PBQ đồng dạng tam giác PQK ( g.g )
\(\Rightarrow\dfrac{PB}{PK}=\dfrac{PQ}{QK}\)
\(\Leftrightarrow\dfrac{PB}{8}=\dfrac{6}{10}\) \(\Leftrightarrow\dfrac{PB}{8}=\dfrac{3}{5}\)
\(\Leftrightarrow5PB=24\) \(\Leftrightarrow PB=\dfrac{24}{5}cm\)
c. Xét tam giác PBQ và tam giác PBK, có:
\(\widehat{PBQ}=\widehat{PBK}=90^0\)
\(\widehat{PQB}=\widehat{BPK}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác PBQ đồng dạng tam giác PBK ( g.g )
\(\Rightarrow\dfrac{PB}{BK}=\dfrac{QB}{PB}\)
\(\Leftrightarrow PB^2=BK.QB\)
Đúng 2
Bình luận (0)












