Vẽ đoạn thẳng DE 8cm. F là điểm nằm giữa D và E, biết DF = 5cm. Lấy K là trung điểm của DE. Tính KE

Những câu hỏi liên quan
mình cần gấp chiều đi học rồi
1. cho 3 điểm d,e,f thẳng hàng và điểm e nằm giữa 2 điểm d và f . biết de= 5cm, ef= 2cm
a, tính độ dài đoạn df
b, gọi m,n tương ứng là trung điểm của các đoạn thẳng de, ef . tính độ dài mn
a, Ta có : e nằm giữa hai điểm d và f
=> de + ef = df
=> df = 5 + 2 = 7cm
b, Vì m là trung điểm của de
=> dm = me = de : 2 = 5 : 2 = 2,5cm
Vì n là trung điểm của ef
=> en = nf = ef : 2 = 2 : 2 = 1cm
Mà e nằm giữa m và n
=> me + en = mn
=> mn = 2,5 + 1 = 3,5cm
Đúng 0
Bình luận (0)
trên tia ox xác định 2 điểm e và fsao cho oe=5cm of=8cm
a)trong 3 điểm ở,e,f điểm nào nằm giữa 3 điểm còn lại?vì sao?
b)tính độ dài đoạn thẳng ef
c)trên tia đối của tia ox lấy điểm d sao cho od=1cmtinh đoạn de
đ)so sánh độ dài đoạn thẳng de và df
a ) Trg ba điểm o,e,f điểm e nằn giưã hai điểm còn lại vì : of = oe + ef
b) ta có : of + oe = ef ( điểm e nằn giữa o và f )
=> ef = of - oe
ef = 8 - 5 = 3 cm
d) vì ef nhỏ hơn de (3cm<4cm) nên ef<de
1.Trên tia Dx lấy 2 điểm E và F sao cho DE 2 cm; DF 6cma) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?b) Tính độ dài đoạn thẳng EFc) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB 5cm; AC 8cma)Tính độ dài đoạn thẳng BCb) trên tia đối của tia By vẽ đoạn thẳng BM 2cm. So sánh 2 đoạn thẳng AB và MC
Đọc tiếp
1.Trên tia Dx lấy 2 điểm E và F sao cho DE= 2 cm; DF= 6cm
a) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?
b) Tính độ dài đoạn thẳng EF
c) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF
2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB= 5cm; AC= 8cm
a)Tính độ dài đoạn thẳng BC
b) trên tia đối của tia By vẽ đoạn thẳng BM= 2cm. So sánh 2 đoạn thẳng AB và MC
1.Trên tia Dx lấy 2 điểm E và F sao cho DE 2 cm; DF 6cma) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?b) Tính độ dài đoạn thẳng EFc) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF( có vẽ hình)2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB 5cm; AC 8cma)Tính độ dài đoạn thẳng BCb) trên tia đối của tia By vẽ đoạn thẳng BM 2cm. So sánh 2 đoạn thẳng AB và MC(có vẽ hình)
Đọc tiếp
1.Trên tia Dx lấy 2 điểm E và F sao cho DE= 2 cm; DF= 6cm
a) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?
b) Tính độ dài đoạn thẳng EF
c) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF
( có vẽ hình)
2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB= 5cm; AC= 8cm
a)Tính độ dài đoạn thẳng BC
b) trên tia đối của tia By vẽ đoạn thẳng BM= 2cm. So sánh 2 đoạn thẳng AB và MC
(có vẽ hình)
Vẽ đoạn thẳng EF = 8cm. Lấy điểm D là trung điểm của EF. Tính DE, DF
vì D là trung điểm của EF
`=>DE=DF=1/2EF=1/2*8=4(cm)`
Đúng 2
Bình luận (0)
Do D là trung điểm của EF
\(\Rightarrow DE=DF=\dfrac{EF}{2}=\dfrac{8}{2}=4cm\)
Đúng 1
Bình luận (0)
Cho tam giác cân DEF (DE = DF). Gọi N và M lần lượt là trung điểm của DE và DF, kẻ DH vuông góc với EF tại H.
1. Chứng minh HE = HF. Giả sử DE = DF = 5cm, EF = 8cm. Tính độ dài đoạn DH.
2. Chứng minh EM = FN và góc DEM = DFN
3. Gọi giao điểm của EM và FN là K. Chứng minh KE = KF.
4. Chứng minh ba điểm D, K, H thẳng hàng.
cho đoạn thẳng DE = 15cm gọi F là điểm nằm giữa DE sao cho 2DF = 3DE tính DF và DE
cho đoạn thẳng DE = 15cm gọi F là điểm nằm giữa DE sao cho DF-EF =3cm tính DF và EF
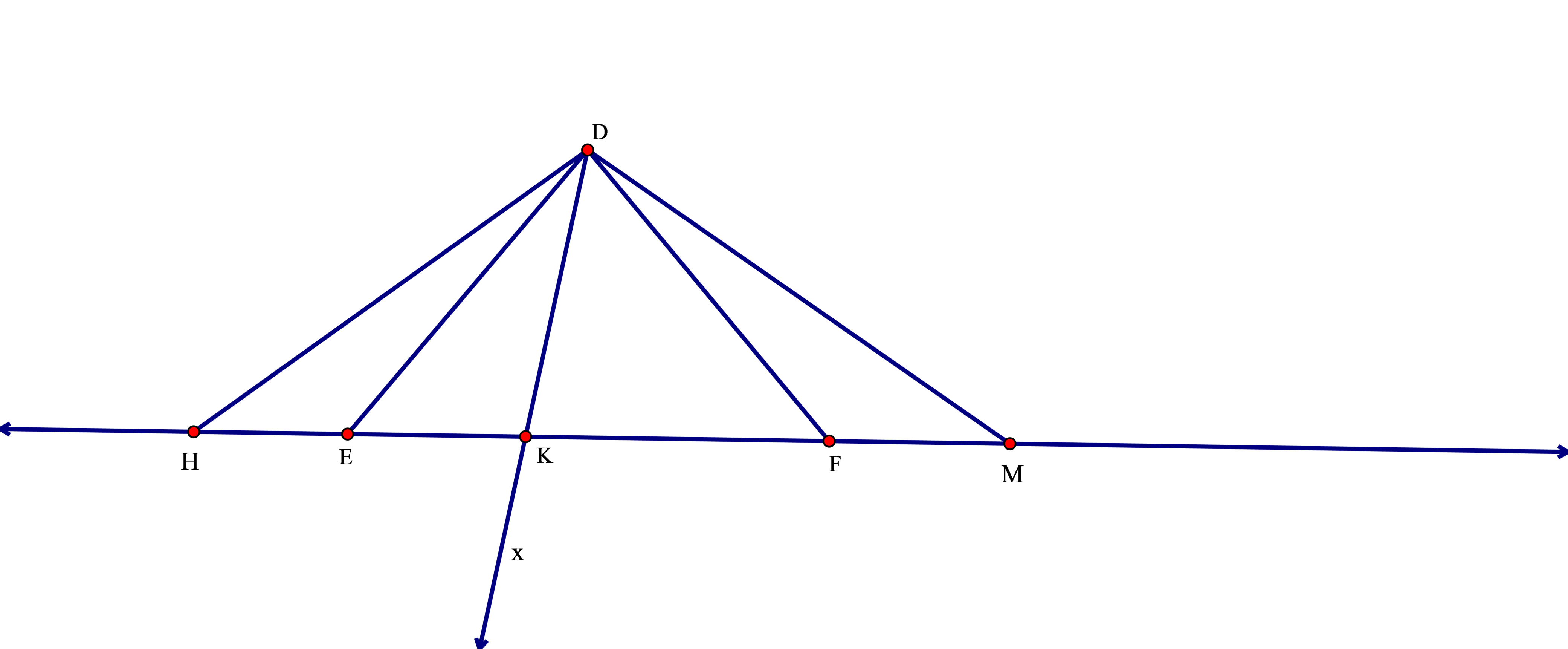
Vẽ hình theo yêu cầu sau:a) Lấy 3 điểm D, E, F không thẳng hàngb) Vẽ đoạn thẳng DE, DF c) Vẽ tia Dx cắt đường thẳng EF tại K nằm giữa E và F d) Vẽ đoạn thẳng DH cắt tia FE tại H Vẽ đoạn thẳng DM cắt tia EF tại M.
Đọc tiếp
Vẽ hình theo yêu cầu sau:
a) Lấy 3 điểm D, E, F không thẳng hàng
b) Vẽ đoạn thẳng DE, DF
c) Vẽ tia Dx cắt đường thẳng EF tại K nằm giữa E và F
d) Vẽ đoạn thẳng DH cắt tia FE tại H
Vẽ đoạn thẳng DM cắt tia EF tại M.
Cho tam giác DEF vuông tại D có DE 3cm, EF 5cma) Tính độ dài cạnh DE và so sánh các góc của tam giác DEFb) Trên tia đối của tia DE lấy điểm K sao cho D là trung điểm của đoạn thẳng EK. Chứng minh tam giác EKF cânc) Gọi I là trung điểm của cạnh EF, đường thẳng KI cắt cạnh DF tại G. Tính GFd) Đường trung trực d của đoạn thẳng DF cắt đường thẳng KF tại M. Chứng minh ba điểm E, G, M thẳng hàng
Đọc tiếp
Cho tam giác DEF vuông tại D có DE= 3cm, EF= 5cm
a) Tính độ dài cạnh DE và so sánh các góc của tam giác DEF
b) Trên tia đối của tia DE lấy điểm K sao cho D là trung điểm của đoạn thẳng EK. Chứng minh tam giác EKF cân
c) Gọi I là trung điểm của cạnh EF, đường thẳng KI cắt cạnh DF tại G. Tính GF
d) Đường trung trực d của đoạn thẳng DF cắt đường thẳng KF tại M. Chứng minh ba điểm E, G, M thẳng hàng
a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)
Đúng 0
Bình luận (0)