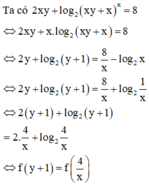tìm hai số x,y thõa mãn điều kiện : x-y=3 và xy=10

Những câu hỏi liên quan
a) Tìm các nghiêm nguyên dương của phương trình: 4xy - 10 x + 6y = 22
b) Cho hai số x,y thõa mãn điều kiện: x - y = 1. Chứng minh rằng: \(xy+1\ge\frac{3}{4}\)
Câu a bạn giản ước đì rồi táchr a nhé
b) Ta có (x+y)2>=0
=>x2+y2+2xy>=0
=>x2+y2>= -2xy
=> x2+y2+x2+y2 >=x2+y2-2xy=(x-y)2=1
=>2x2+2y2>=1
=>2x2+2y2+2>=3
=> \(\frac{2x^2+2y^2+2}{4}>=\frac{3}{4}\)
=>\(\frac{x^2+y^2+1}{2}>=\frac{3}{4}\)
Mà (x-y)2=1 => x2+y2-2xy=1
=>x2+y2-1=2xy
=.\(xy=\frac{x^2+y^2-1}{2}\)
=> \(xy+1=\frac{x^2+y^2-1}{2}+1=\frac{x^2+y^2+1}{2}\)
=> xy+1>=3/4
Đúng 0
Bình luận (0)
Tìm các cặp số nguyên x,y thõa mãn điều kiện x^5+y^2=xy^2+1
tìm hai số nguyên x và y thõa mãn: x+y+xy=4x
Cho hai số thực x, y dương thõa mãn điều kiện x2 + y2 - xy = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức : P = x2 + y2. (Trích đề thi HSG toán 9 tỉnh Bình Định năm học 2012-2013)
Cho hai số thực dương x, y thõa mãn điều kiện
2
x
y
+
log
2
x
y
+
x
x
8
. Tìm giá trị nhỏ nhất của
P
2
x
2
+
y
A.
P
m
i...
Đọc tiếp
Cho hai số thực dương x, y thõa mãn điều kiện 2 x y + log 2 x y + x x = 8 . Tìm giá trị nhỏ nhất của P = 2 x 2 + y
A. P m i n = 3
B. P m i n = 2 3 - 1
C. P m i n = 5
D. P m i n = 3 4 3 - 1
Cho hai số thực dương x,y thõa mãn : x^4+y^4+1/xy=xy + 2
Tìm GTLN VÀ GTNN của P=xy
tìm tất cả các số nguyên dương thõa mãn điều kiện xy+2x-y=5
Ta có xy+2x-y=5<=>x(y+2)-(y+2)=3 <=>(x-1)(y+2)=3 .DO x\(\in\)Nsao =>x-1 thuộc n sao =>x-1 thuộc ước của 3
bạn tự làm tiếp nha nhớ k mk đó
Đúng 0
Bình luận (0)
xy+2x-y=5
<=>x(y+2)-y-2=5-2
<=>x(y+2)-(y+2)=3
<=>(y+2)(x-1)=3
<=>y+2 và x-1 E Ư(3)
<=>......
Đúng 0
Bình luận (0)
Tìm m biết x,y là các số nguyên thoả mãn điều kiện xy=3 và x+y=-(m+2)
tìm tổng các số nguyên x thõa mãn điều kiện |x-1|-3<10
/x-1/-3<10 <=> /x-1/<13
=> /x-1/ thuộc {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
=> x={1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}
Đúng 0
Bình luận (0)