Cho tam giác ABC nhọn. AB < AC.Đường cao AH. Điểm D nằm ngoài tam giác ABC sao cho AD vuông góc với AB và AD = AB. Điểm E cũng nằm ngoài tam giác ABC, AE vuông góc với AC, AE = AC. AH cắt DE tại I. CMR: I là trung điểm của DE.

Những câu hỏi liên quan
cho tam giác ABC về phía ngoài của tam giác ta kẻ Ax vuông góc vơi AB, Ay vuông góc với AC. Trên Ax lấy điểm D sao cho AD=AB, trên Ay lấy điểm E sao cho AE=AC. Nối D với E/ Kẻ AH vuông góc với BC tại H. đường thẳng AH cắt DE tại I. Chứng minh I là trung điểm của DE
cho tam giác abc về phía ngoài của tam giác ta kẻ ax vuông góc vơi ab, ay vuông góc với ac. trên ax lấy điểm d sao cho ad=ab, trên ay lấy điểm e sao cho ae=ac. nối d với e. Gọi m là trung điểm của DE. kẻ ah cắt bc tại h. chứng minh ah vuông góc với bc
Cho tam giác nhọn ABC . Vẽ AD vuông góc AB va AD=AB ( D và C nằm khác phía đối với AB ) . Vẽ AE vuông góc AC và AE=AC ( E và B nắm khác phía đối với AC ) Vẽ AH vuông góc BC ( H thuộc BC ) . Kẻ đường thẳng từ D và E cắt AH lần lượt tại I và K . Gọi M là giao điểm của DE và AH
a) CM tam giác ABH = DAI
b ) CM tam giác ACH = EAK
c ) CM MD = ME
nhanh nhanh nha các bạn mình cần gấp
cho tam giác ABC vuông tại A ( AB < AC) đường cao AH. Trên AC lấy E sao cho AH = AE. Từ E kẻ đường vuông góc với AC, cắt BC tại D
a,CMR tam giác AHD = tam giác AED
b, so sánh DH và DC
c,Gọi K là giao điểm của DE và AH. CM AD vuông góc vơi KC
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: DH=DE
DE<DC
=>DH<DC
c: Xét ΔAKC có
CH,KE là đường cao
CH căt KE tại D
=>D là trực tâm
=>AD vuông góc KC
Đúng 1
Bình luận (0)
cho tam giác ABC có A là góc nhọn. Bên ngoài tam giác vẽ tia Ax vuông góc với BC. Trên tia Ax lấy điểm D sao cho AD bằng AB . Vẽ tia Ay vuông góc với AC , trên tia Ay lấy điểm E sao cho AE bằng AC. Gọi I là trung điểm của DE, IA cắt BC tại H. cmr AH vuông góc với BC
Cho tam giác ABC có ba góc nhọn.Vẽ đoạn thẳng AD vuông góc với AB,AD=AB( D và C nằm về hai phía đối với AB).Vẽ đoạn thẳng AE vuông góc với AC,AE=AC(E và B nằm về hai phía đối với AC ).Kẻ AH vuông góc với đường thẳng BC tại H.Kẻ DI và EK cùng vuông góc với đường thẳng AH(I và K thuộc đường thẳng AH) .CM rằng: DI=EK, DE và KI cắt nhau tại trung điểm của mỗi đường
cho tam giác abc vuông tại A (AB<AC) ke Ah vuông với bc tại h trê cạnh ac lấy điểm d sao cho ad=ah gọi e là trung điểm của hd tia ae cắt bc tai f cm a) tam giác ahe= tam giác ade và ae vuông tại hd b) tam giác ahf = tam giác adf c) góc dfc= góc abc
cho tam giác abc vuông tại A (AB<AC) ke Ah vuông với bc tại h trê cạnh ac lấy điểm d sao cho ad=ah gọi e là trung điểm của hd tia ae cắt bc tai f cm a) tam giác ahe= tam giác ade và ae vuông tại hd b) tam giác ahf = tam giác adf c) góc dfc= góc abc
Đúng 0
Bình luận (0)
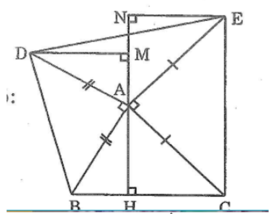
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: MN đi qua trung điểm của DE
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
Đúng 0
Bình luận (0)
Nhờ mọi người làm nhanh giùm mai cần rồi
Cho tam giác ABC nhọn, vẽ về phía ngoài của tam giác ABC, các tam giác vuông ABD và tam giác vuông ACE có AB=AD, AC=AE. CM:a) tam giác ABE= tam giác ACD b)DC vuông góc BE c)Kẻ AH vuông góc với BC cắt DE tại M.CM:M là trung điểm của DE.
Xem chi tiết
cho mk hỏi tam giac vông thì vuông tai đâu vậy chứ đề vạy thì mk chịu thôi
















