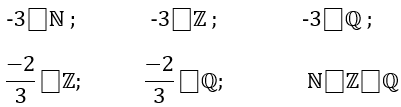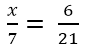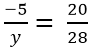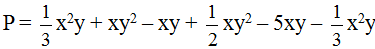bài 59 60 sgk toán lớp 7 trang 132 133 tập 1
?1 sgk trang 135

Những câu hỏi liên quan
Bài 1 (trang 7 SGK Toán 7 Tập 1): Điền kí hiệu (∈, ∉, ⊂) thích hợp vào ô vuông
giải theo đúng 1 bài tìm x cho mik nha
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
Đúng 3
Bình luận (0)
a) x/7=6/21
x.21=6.7
x.21=42
x=42:21
x=2
b) -5/y=20/28
y.20=(-5).28
y.20= -140
y= (-140):20
y= -7
TICK CHO MÌNH NHA^^
Đúng 1
Bình luận (0)
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
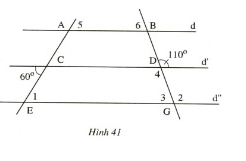
Hình 41 cho biết d // d' // d'' và hai góc 60o, 110o. Tính các góc E1; G2; G3; D4; A5; B6
1) Tính góc ∠E1
Ta có d’//d” (gt)
⇒ ∠C = ∠E1 ( So le trong)
⇒ ∠E1 = 600 vì ∠C = 600
2) Tính ∠G3
Ta có d’//d”
⇒ ∠G2 = ∠D (Đồng vị)
⇒ ∠G1 = 1100
3) Tính ∠G3
Vì ∠G2 + ∠G3 = 1800 (kề bù)
⇒ ∠G3 = 700
4) Tính ∠D4
∠D4 = ∠D (Đối đỉnh)
⇒ ∠D4 = 1100
5) Tính ∠A5
Ta có d//d”
⇒ ∠A5 = ∠ E1 (Đồng vị)
⇒ ∠A5 = 600
6) Tính ∠B6
Ta có d//d”
⇒ ∠B6 = ∠G3 (Đồng vị)
⇒ ∠B6 = 700
Đúng 0
Bình luận (0)
giúp mik với
Đề là: bài 3/ trang 108
Lớp 7 sgk toán tập 1
TL
a) Ta có ˆBIKBIK^ là góc ngoài tại đỉnh II của ΔBAIΔBAI.
Nên ˆBIK=ˆBAI+ˆABI>ˆBAIBIK^=BAI^+ABI^>BAI^
Mà ˆBAK=ˆBAIBAK^=BAI^
Vậy ˆBIK>ˆBAKBIK^>BAK^ (1)
b) Ta có ˆCIKCIK^ là góc ngoài tại đỉnh II của ΔAICΔAIC
nên ˆCIK=ˆCAI+ˆICA>ˆCAICIK^=CAI^+ICA^>CAI^
Hay ˆCIK>ˆCAICIK^>CAI^ (2)
Từ (1) và (2) ta có:
ˆBIK+ˆCIK>ˆBAK+ˆCAIBIK^+CIK^>BAK^+CAI^
⇒ˆBIC>ˆBAC⇒BIC^>BAC^.
Hok tốt nha bn
#Kirito
gõ lên cốc cốc học tập nhé bạn
yêu rùi cưới bạn nhé
Xem thêm câu trả lời
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
JUP
Giả sử 
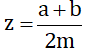
Xem thêm câu trả lời
Giả sử 
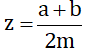
Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)
Đúng 0
Bình luận (0)
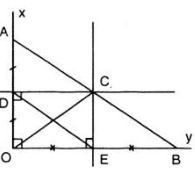
Gửi trần quang nhật nè:
Bài giải:
Lời giải
c) Chứng minh CA CB
- Vì C nằm trên đường trung trực của OA nên CA CO (3)
- Vì C nằm trên đường trung trực của OB nên CB CO (4)
Từ (3) và (4) suy ra: CA CB (đpcm).
Đọc tiếp
Gửi trần quang nhật nè:
Bài giải:
Lời giải
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
Đúng 0
Bình luận (0)
Xem thêm câu trả lời