cho hình thang ABCD, AB=8cm. đường trung bình hình thang cắt AC, BD tại I,K. biết IK=2cm. tính CD

Những câu hỏi liên quan
Cầu 4. (2 điểm). Cho hình thang ABCD (AB // CD) . Từ trung điểm M của cạnh bên AD, vẽ một đường thẳng song song với hai đáy lần lượt cắt BD tại I: AC tại K: BC tại N. Tính độ dài các đoạn thẳng MI. KN. IK biet AB=8cm : CD = 12 cm
Cho hình thang ABCD , AB song song CD.Gọi E,F là trung điểm của AD , BC . È cắt BD , AC tại I và K
a) CMR;I,K là trung điểm của BD,AC
b)Cho AB =8cm ,CD= 12Cm.Tính EI , IK,KF
Cho hình thang cân ABCD (AB//CD) và AB < CD, DA cắt CB tại I. AC cắt BD tại K. Chứng minh IK là trục đối xứng của hình thang ABCD.
Cho hình thang ABCD(AB//CD), AC cắt BD tại O
a, chứng minh:OA.OD=OB.OC. Nếu AB=4cm, DC=8cm, DC=6cm. Tính OA?
b, Gọi M là trung điểm BC,AM cắt BD tại I, BM cắt AC tại K. Chứng minh:IK//AB
Cho hình thang ABCD ( AB//CD) M là trung điểm của CD AM cắt BD tại I BM cắt AC tại K a) Cm: IK//AB b )IK cắt AD và BC tại lần lượt là E,F cm:EI=IK=KF
a: Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD=IB/ID
Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KA/KC=KB/KM=AB/CM
KB/KM=AB/CM
AI/IM=AB/MD
mà CM=MD
nên KB/KM=AI/IM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
Xét ΔADM có EI//DM
nên EI/DM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên AI/AM=BK/BM
=>IK/MC=FK/MC=EI/DM
mà MC=DM
nên IK=FK=EI
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB//CD), AB = 5cm, CD = 12cm, BD = 8cm, AC = 15cm
a) Qua B kẻ đường thẳng // AC cắt CD tại E
+) Tính BE
+) Tính góc DBE
b) Tính diện tích hình thang ABCD.
Cho hình thang ABCD (AB//CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, EF cắt AC tại K.
a) CMR: AK=KC; BI=ID
b) Biết AB=6cm, CD=10cm.Tính EI, KF, IK
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.
a) Chứng minh rằng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.
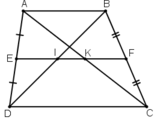
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm
Đúng 2
Bình luận (0)
cho hình thang ABCD có đáy bé AB bằng 6cm và đáy lớn CD dài hơn đáy bé AB là 8cm. chiều cao AH của hình thang bằng trung bình cộng của hai đáy.
a) tính chiều cao AH của hình thang ABCD.
b) tính diện tích hình thang ABCD.
c) hai đường chéo AC và BD cắt nhau tại K.
so sánh diện tích hai tam giác AKD và BKC.
a) Đáy lớn hình thang là:
8 + 6 = 14 cm
b) Chiều cao AH là:
( 6 + 8 ) : 2 = 7 cm
Diện tích hình thang ABCD là:
8 x 6 = 48 cm2
c) bạn tự làm nha!
Đúng 1
Bình luận (0)














