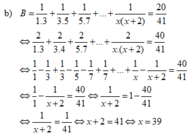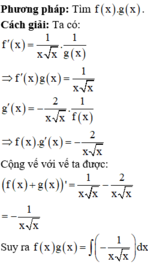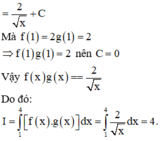78 x ab : 1xx = 1xx : 23 x yy
Những câu hỏi liên quan
Tìm x, biết:
b) 1 1 . 3 + 1 3 . 5 + 1 5 . 7 + . . . + 1 x x + 2 = 20 41
cho biểu thức √x√x−1+3√x−1−6√x−4x−1−1xx−1+3x−1−6x−4x−1−1
a, rút gon A
b,Tìm x để A = -2
c,Tìm x nguyên để A cũng là số nguyên
Tìm giá trị của x để giá trị của các biểu thức trong bài tập 62 bằng 0.
2 x 2 + 1 x x - 1
Biểu thức 2 x 2 + 1 x x - 1 xác định khi x ≠ 0 và x ≠ 1
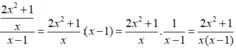
Ta có: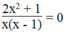 
khi
2
x
2
+
1
= 0 và x(x – 1)
≠
0
Ta có: 2 x 2 ≥ 0 nên 2 x 2 + 1 ≠ 0 mọi x.
Không có giá trị nào của x để biểu thức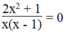 
có giá trị bằng 0.
Đúng 0
Bình luận (0)
29 tháng 6 2021 lúc 7:55
* Cho biểu thức:
B=(1x−√x+√xx−1):x√x−1x√x−√x(1x−x+xx−1):xx−1xx−x ( với x>0, x≠1)
a. Rút gọn B
b. Tìm x để B =12
Bạn cần viết đề bài bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 1
Bình luận (0)
Tìm x:
a. 2-x=1
b. 10+x=24
c. 15:x=5
d. 1xX=3
a. 2-x=1
x=2-1
x=1
b. 10+x=24
x=24-10
x=14
c. 15:x=5
x=15:5
x=3
d. 1xX=3
X=3:1
X=3
Đúng 0
Bình luận (0)
a) \(2-x=1\)
\(\Rightarrow x=1\)
b) \(10+x=24\)
\(\Rightarrow x=14\)
c) \(15:x=5\)
\(\Rightarrow x=3\)
d) \(1\times x=3\)
\(\Rightarrow x=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định: 2 x 2 + 1 x x - 1
Biểu thức 2 x 2 + 1 x x - 1 xác định khi: x ≠ 0 và x – 1 ≠ 0 ⇔ x ≠ 0 và x ≠ 1
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 1.
Đúng 0
Bình luận (0)
Cho hàm số f(x) và g(x) có đạo hàm trên [1;4] và thỏa mãn hệ thức sau với mọi
x
∈
1
;
4
f
1
2
g
1
2
f...
Đọc tiếp
Cho hàm số f(x) và g(x) có đạo hàm trên [1;4] và thỏa mãn hệ thức sau với mọi x ∈ 1 ; 4
f 1 = 2 g 1 = 2 f ' x = 1 x x . 1 g x ; g ' x = - 2 x x . 1 f x . Tính I = ∫ 1 4 f x g x d x
A. 6
B. 4
C. 2
D. 7
Cho hàm số f (x) liên tục và có đạo hàm trên
1
2
;
1
thỏa mãn f (x)
1
x
x
-
2
. Biết f(1) 1, f(
ln
1...
Đọc tiếp
Cho hàm số f (x) liên tục và có đạo hàm trên
1
2
;
1
thỏa mãn f ' (x) =
1
x
x
-
2
. Biết f(1) = 1, f( =
ln
1
a
ln
3
+
b
,
(
a
,
b
∈
). Tổng a + b bằng
A. 2
B. 3
C. - 2
D. - 3
Đáp án B
Cách giải:
f ' (x) = 1 x x - 2
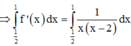
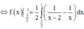
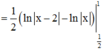
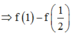
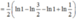
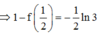
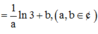
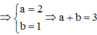
Đúng 0
Bình luận (0)
Cho hàm số f ( x ) = x - 1 x x
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
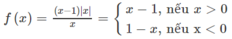
Hàm số này có tập xác định là R \ {0}
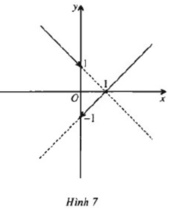
Từ đồ thị (H.7) dự đoán f(x) liên tục trên các khoảng (−∞;0), (0; +∞) nhưng không liên tục trên R. Thật vậy,
- Với x > 0, f(x) = x − 1 là hàm đa thức nên liên tục trên R do đó liên tục trên (0; +∞)
- Với x < 0, f(x) = 1 – x cũng là hàm đa thức nên liên tục trên R do đó liên tục trên (−∞; 0)
Dễ thấy hàm số gián đoạn tại x = 0 vì
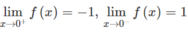
Đúng 0
Bình luận (0)