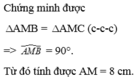Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC. Biết AB = 13, AM = 12. Tính độ dài cạnh BC

Những câu hỏi liên quan
cho tam giác ABC cân tại A, M là trung điểm của BC. CMR: a, tam giác AMB= tam giác AMC. b, tính độ dài AM biết AB=10cm; BC=12cm c, kẻ đường trung tuyến CE cắt AM tại D. gọi I là điểm cách đều 3 cạnh của tam giác ABC. CMR: I;D;M thẳng hàng.
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A có AB =10cm, BC = 12cm. Gọi M là trung điểm của BC. Tính độ dài AM.
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.Câu 2: Cho hình thang cân ABCD, đáy lớn CD10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.Câu 4: Cho tam giác ABC vuông tại A, ABAC; gọi I là giao điểm các đường phân giác, M là...
Đọc tiếp
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
Đúng 1
Bình luận (0)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác ABC vuông tại A,AB12 cm BC13 cm .Gọi M, N lần lượt là trungđiểm của AB và BCa) Chứng minhMN vuông góc AB b) Tính độ dài MNBài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi Ilà giao điểm của AP và MN. C/m: a) IA IP b) IM IN.Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểmcủa DH, M là trung điểm của HC.C/m:a) IM vuông góc AD b) AI vuông góc DM.
Đọc tiếp
Bài 5: Cho tam giác ABC vuông tại A,
AB=12 cm BC=13 cm .
Gọi M, N lần lượt là trung
điểm của AB và BC
a) Chứng minh
MN vuông góc AB
b) Tính độ dài MN
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểm
của DH, M là trung điểm của HC.
C/m:a) IM vuông góc AD b) AI vuông góc DM.
Cho tam giác ABC vuông tại a có ab 6cm BC 10cm a tính độ dài cạnh ac và so sánh các góc của tam giác ABC b trên tia đối của tia ab lấy điểm d sao cho ab ad gọi k là trung điểm của BC đường thẳng dk cắt ac tại m chứng minh BC BD và tính độ dài cạnh am
Xem chi tiết
Cho Δ ABC cân tại A. Gọi M là trung điểm của cạnh BC. Cho biết AB=13 cm, AM= 12cm. Tính cạnh BC
Cho tam giác ABC vuông tại A có AB = 3cm. Gọi M là trung điểm của BC, N là điểm thuộc cạnh AB sao cho NA = 2NB. Biết rằng AM vuông góc với CN. Tính độ dài cạnh AC
\(\Delta ABC\) vuông tại A
AM là đường trung tuyến => AM=MB=MC=\(\frac{BC}{2}\)
=> \(\Delta AMB\)cân tại M, \(\Delta AMC\) cân tại M
Xét \(\Delta AMB\) và \(\Delta AMC\) có
AM chung
MB=MC
=>\(\Delta AMB=\Delta AMC\)
=>AB =AC =3 cm( 2 cạnh trương ứng)
hok tốt
AC= 3 cm ấy
Cho tam giác ABC vuông ở A. Gọi điểm M, N thứ tự là trung điểm của cạnh BC, AB. AM gặp CN tại điểm O. Biết AB = 30cm. Tính độ dài chiều cao OH của tam giác AOC
Bài 3. (3 điểm) Cho tam giác ABC cân, biết AB = 10cm, BC = 5cm có độ dài 3 cạnh của
tam giác là 3 số nguyên dương.
a) Tính độ dài cạnh AC và chứng minh rằng tam giác ABC cân tại A.
b) Gọi M, N lần lượt là trung điểm của AB và AC. Chứng minh ABN ACM
c) Chứng minh AB+BC>BN+CM
a: AB+BC>AC>AB-BC
=>15>AC>5
=>AC=10(cm)
=>ΔABC cân tại A
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
Đúng 1
Bình luận (0)